Hvordan løse kvadratiske ulikheter

1. 1
   Trinn 1. Transformere ulikheten i en trinomial f (x) på venstre side og la 0 på høyre side.
   • Eksempel. Denne ulikhet: x (6 x + 1) <15 vil bli omdannet til en trinomial i x: f (x) = x ² 6 + x - 15 <0.
2. 2
   Trinn 2. Løs likningen for å få de virkelige røttene. Du kan bruke noen av disse metodene. Generelt kan en kvadratisk ha null, én eller to reelle røtter.
   • Bruk den kvadratiske formelen (alltid fungerer)
   • Factoring (hvis røttene er rasjonelle)
   • Fylle plassen (alltid fungerer)
   • Grafer (anslag)
   • Diagonal sum metode (snarvei for factoring). Å vite hvordan du skal bruke den nye Diagonal Sum Method, kan du lese artikkelen med tittelen: "Hvordan løse kvadratiske likninger ved Diagonal Sum Method" på denne Google webområde.
3. 3
   Trinn 3. Løs andregradsulikheten, basert på verdiene av de to reelle røtter.
   • Du kan velge en av de to følgende metoder:
     • Metode 1: Bruke tallinja og test punkts metoden. De to reelle røtter er plottet på et antall linje. De delte linjen i ett segment og to stråler. Bruk alltid opprinnelsen O som test punkt. Innbytter x = 0 i den gitte andregradsulikheten. Hvis det er sant, da opprinnelsen ligger på den sanne segment (eller den sanne stråle).
     • Note. Ved denne metoden, kan du bruke en dobbel nummer-linje, eller enda en trippel tall-linje, for å løse systemer av to eller tre kvadratiske ulikheter i én variabel.
     • Metode 2. Ved hjelp av en Theorem på Logg av f (x) hvis algebraisk metode er valgt. Studenter studerer når teoremet utviklingen deretter bruke den til å løse ulike kvadratiske ulikheter.
       • Teorem om Logg av f (x):
         • Mellom to reelle røtter, har f (x) motsatt fortegn av en. Det betyr:
         • Mellom de to reelle røtter, er f (x) er positiv hvis en negativ
         • Mellom de to reelle røtter, er f (x) negativ hvis a er positiv.
         • Du kan forstå dette teoremet ved å se på kryss av parabelen grafen til funksjonen f (x) og x-aksen. Hvis a er positiv, er parabelen oppover. Mellom de to x-skjæringspunkter, er en del av parabelen under x-aksen, det vil si f (x) er negativ i dette intervallet (motsatt fortegn til a).
         • Denne metoden kan være hurtigere enn antallet lineært ettersom den ikke krever å trekke antallet linjen hver gang. I tillegg hjelper det å sette opp et skilt Table i å løse systemer av kvadratiske ulikheter ved algebraisk tilnærming.
4. 4
   Trinn 4. Uttrykk svaret (eller løsning-set) i form av intervaller.
   • Eksempler på intervaller:
   • (A, b), åpent intervall, de to endepunktene a og b ikke er inkludert
   • [A, b], lukket intervall, blir de to endepunktene inkluderes
   • (-Uendelig, b], halvt lukkede intervall, blir endepunkt b inkludert.
     • Note 1. Hvis likningen ikke har reelle røtter, (Diskriminantfunksjoner D <0), er f (x) alltid positive (eller alltid negativ) avhengig av tegn på en betydningen at løsningen settet vil enten være tom eller hele reelle tallet linje. Hvis discriminant lik null (dvs. den kvadratiske har en dobbel rot), så løsningen kan være tom, et enkelt punkt, alle Reals unntatt ett enkelt punkt, eller alle Reals.
   • Eksempel: Løs f (x) = 15x ^ 2 - 8x + 7> 0.
   • Løsning. Den Diskriminantfunksjoner D = b ^ 2 - 4ac = 64-420 <0. Det er ingen reelle røtter. Siden a er positiv, er f (x) alltid positive (> 0) uavhengig av verdiene av x. Ulikheten er alltid sant.
   • Eksempel. Løs f (x) =-4x ^ 2 - 9x - 7> 0.
   • Løsning. Den Diskriminantfunksjoner D = 81-112 <0. Det er ingen reelle røtter. Siden a er negativ, er f (x) alltid negativ, uavhengig av verdiene av x. Ulikheten er ikke alltid sant.
     • Note 2. Når den ulikheten har en ekstra lik (=) sign (større eller lik, mindre eller lik), bruker lukket intervaller som [-4,10] for å indikere at de to ende-punkter er inkludert i løsningen innstilt. Hvis ulikheten har strengt større enn eller mindre enn strengt, bruke åpne intervaller liknende (-4, 10) når endepunktene er utelatt.

Eksempel 1

1. 1
   Løs: 15> 6 x ² + 43 x.
2. 2
   Transformere ulikheten i en trinomial i x. f (x) = -6 x ^2-43 x + 15> 0.
3. 3
   Løs f (x) = 0 ved hjelp av den diagonale summen metoden.
   • Rule of skiltet sier de to røttene har motsatt fortegn siden konstantleddet og koeffisienten til x ² har motsatt fortegn.
   • Skriv ned sannsynlig røtter-sett: {-3/2, 5/3}, {-1 / 2, 15/3}, {-1 / 3, 15/2}. Produktet av numerators er den konstante term (15), og produktet av den denominators er koeffisienten av den x ² uttrykket: 6 (denominators alltid positiv).
   • Beregn den diagonale summen av hver kandidat for rot parene ved tilsetning av de første tellerens ganger den andre nevneren til det første nevneren ganger den andre telleren. For dette eksempel, de diagonale summene er (-3) * (3) + (2) * (5) = 1, (-1) * (3) + (2) * (15) = 27, og (-1 ) * (2) + (3) * (15) = 43. Siden den diagonale sum av de faktiske røtter må være lik - b * sign (a) der b er koeffisienten til x og a er koeffisienten til x ^2, vil vi det tredje settet, men må negere begge løsningene. De to reelle røtter er: {1/3, -15 / 2}
4. 4
   Bruk teorem til å løse ulikheten. Mellom to de virkelige røttene
   • f (x) er positiv, motsatt fortegn til a = -6. Utenfor dette intervallet, er f (x) negativ. Siden den opprinnelige ulikheten hadde streng ulikhet, bruker den åpne intervall for å utelukke endepunktene der f (x) = 0.
     • Løsningen sett er intervallet (-15 / 2, 1/3).

Eksempel 2

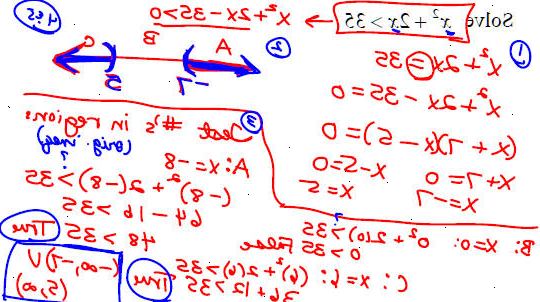
1. 1
   Løs: x (6x 1) <15.
2. 2
   Transformere ulikheten inn: f (x) = 6x ^ 2 + x - 15 <0.
3. 3
   De to røtter har motsatt fortegn.
4. 4
   Skriv ned sannsynlig rot-sett: (-3 / 2, 5/3) (-3 / 3, 5/2).
   • Den diagonale summen av første settet er 10-9 = 1 = b.
   • De to reelle røtter er 3/2 og -5/3.
5. 5
   Velg antall linje-metoden for å løse ulikheten.
6. 6
   Velger som test-point opprinnelsen O. Substitute x = 0 inn i ulikhet. Det viser: - 15 <0. Det er sant!. Opprinnelsen er plassert på den sanne segmentet og oppløsningen set er intervallet (-5 / 3, 3/2).
7. 7
   Metode 3. Løse kvadratiske ulikheter ved grafisk fremstilling.
   • Konseptet med denne grafiske metode er enkel. Når parabelen diagram av funksjonen f (x) over x-aksen, så det trinomial er positivt, og omvendt. For å løse kvadratiske ulikheter, trenger du ikke å nøyaktig graf parabelen. Basert på de to reelle røtter, kan du grovt skissere parabel. Bare sørg for at parabelen er riktig bøyd oppover eller nedover.
   • Med denne metoden kan du løse systemer av to eller tre kvadratiske ulikheter ved grafiske to eller tre parabler på samme koordinatsystem.