Fundamental Theorem of Algebra sier at over de komplekse tallene et polynom har så mange røtter som grad sin. Mens, for høy grad polynomer, kan disse ikke alltid bli funnet algebraically, vil de teknikkene her tillater en å finne alle rasjonelle røtter og i gunstige tilfeller, noen av de irrasjonelle eller komplekse røtter. Andre kan anslås numerisk.
Trinn
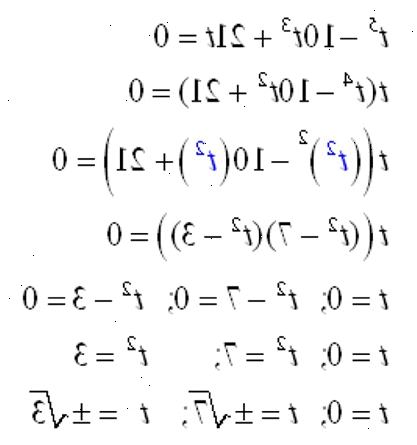
- 1Finn den største felles faktor (GCF). For eksempel, i polynomet 5x ^ 3 + ^ 2 + 15x 100x + 20, er hver enkelt koeffisient et multiplum av 5. Derfor ligningen kan forenkles ved å dele dette ut til å få 5 (x ^ 3 + 3x ^ 2 + 20x + 4) som har nøyaktig de samme røttene som x ^ 3 + 3x ^ 2 + 20x + 4.
- 2Alle kvadratiske (grad 2) polynomer kan løses algebraisk. Faktor det hvis du kan gjøre det raskt. Ellers bruker den kvadratiske formelen. Tips: Se på den delen av likningen kjent som discriminant (den delen b ^ 2-4ac under radikale i den kvadratiske formelen). Sin evaluering forteller deg hva slags løsninger. For eksempel, hvis resultatet er positivt det er to løsninger reelt tall, hvis resultatet er 0 er det bare en løsning fordi den kvadratiske er en perfekt kvadratisk, og hvis den er negativ diskriminant er løsningene komplekse konjugerte (a + bi og a-bi). De er de ligninger hvor i high school algebra klasse forteller de deg de er ikke factorable over reelle tall, også referert til som statsminister. Multipliser (a + bi) (a-bi) = a ^ 2 + b ^ 2 i henhold til våre regelen for "sum av kvadrater."
- 3Bruk Descartes 'styre av tegn til å lære noe om tegn på de virkelige røttene. Denne regelen gir maksimalt antall positive og negative reelle røtter. Det kan også være et multiplum av to færre.
- Telle fortegnendringene (når skiltet endres fra positiv til negativ): + x ^ 2 - x + 6 har to sign endringer som betyr at det er enten to eller null positive nuller (i dette tilfellet null siden den kvadratiske formelen viser både røtter å være kompleks).
- Bytt hver x med en negativ x: (-x) ^ 2 - (-x) + 6. Forenkle dette: x ^ 2 + x + 6 Telle fortegnendringene ot finne antall negative reelle røtter. Dette polynom har null negative nuller.
- 4Prøv den rasjonelle null test. De mulige rasjonelle nuller er P / Q der P deler konstant sikt og Q deler koeffisienten til variabelen med høyest eksponent. Bruk syntetisk divisjon å teste hver kandidat for den rasjonelle røtter. Sørg for at du teste både de positive og negative canditates med mindre du vet fra Descarte styre som enten positive reelle eller negative reelle røtter er umulig.
- 5Hvis du mistenker at din polynom har en dobbel rot, beregne for polynomet og sin første derivat. Hvis GCD er en konstant, så alle dine røtter er tydelig. Hvis GCD har graden større enn en, da har du funnet en faktor som har røtter er flere røtter i den opprinnelige polynomet.
Tips
- Kubikk og quartic formler eksisterer lik den kvadratiske ligningen, men er mye mer komplisert og er ikke ofte anvendt bortsett fra ved datamaskin. Polynomer av grad 5 og høyere er generelt uløselige mindre de kan være tatt.
- Det er mange måter å finne de nuller. Noen av disse verktøyene fungerer bare i noen spesielle tilfeller, og du ofte ikke vet om det hjelper med polynom eller ikke før du prøver det. Derfor er det nyttig å vite så mange triks som du kan for å maksimere sannsynligheten for at minst én av dem vil gjelde.
- Etter å finne noen rot eller faktor, deler du originalen polynom av irreducible polynom av at roten. (Det reduserer graden din og gjør finne de andre røttene enklere.) Hvis du søker etter rasjonelle røtter x ^ 3-1 funn x = 1 da (x ^ 3-1) / (x-1) = x ^ 2 + x + en som inneholder de gjenværende røtter. Dette er også en enkel måte å kontrollere arbeidet. Hvis du tror x = 3 er en løsning, men kan ikke dele (x-3) i den opprinnelige polynomet uten rest, så du har gjort en feil.
- Begrepene røtter, nuller og løsninger alle refererer til verdiene av x som gjør f (x) = 0. De kan brukes interchangably.
- Når du arbeider ut et problem, må du skrive ned hvert trinn og tilbake i løpet av arbeidet for feil.
Advarsler
- Bruk en blyant!
- Vær forsiktig og alltid sørge for at du dobbeltsjekke arbeidet ditt slik at du ikke glipp av de enkle små feil som du kan gå glipp av.
- Hvis du får en imaginær ikke glem at det vil være en null på det tallet og dens comples konjugat. Dersom (x-3i) er en rot, så er det (x 3 I).
- Når syntetisk dele, ikke glem å bruke både positive og negative faktorer.
