Dette er en artikkel om hvordan du faktorisere et 3. grads polynom. Vi vil utforske hvordan å faktor bruke gruppering samt bruke faktorene til fri sikt.
Trinn
Del 1: factoring ved å gruppere
- 1Gruppe polynomet i to seksjoner. Gruppering polynomet i to seksjoner vil gi oss angripe hver del individuelt.
- Si at vi jobber med polynomet x 3 + 3x 2 - 6x - 18 = 0. La oss gruppe den inn (x 3 + 3x 2) og (- 6x - 18)
- 2Finne hva som er vanlig i hver seksjon.
- Ser på (x 3 + 3x 2), kan vi se at x 2 er vanlig.
- Ser på (- 6x - 18), kan vi se at -6 er vanlig.
- 3Faktor på fellesnevnerne ut av de to begrepene.
- Factoring ut x 2 fra det første avsnittet, får vi x 2 (x + 3).
- Factoring ut -6 fra den andre delen, får vi -6 (x + 3).
- 4Hvis hver av de to begrepene inneholder samme faktor, kan du kombinere faktorene sammen.
- Dette gir oss (x + 3) (x 2-6).
- 5Finne løsningen ved å se på røttene. Hvis du har en x 2 i røttene dine, husk at både negative og positive tall oppfylle ligningen.
- Løsningene er tre, og √ 6.
Del 2: factoring ved hjelp av gratis sikt
- 1Omorganisere uttrykket slik det er i form av ax 3 + bx 2 + cx + d.
- La oss si at vi jobber med likningen: x 3 - 4x 2 - 7x + 10 = 0.
- 2Finn alle av faktorene av "d". Den konstante "d" kommer til å være nummer som ikke har noen variabler, for eksempel "x", ved siden av den.
- Faktorene er tallene du kan formere sammen for å få et annet nummer. I vårt tilfelle, hvilke faktorer på 10, eller "d", er: 1, 2, 5, og 10..
- 3Finne en faktor som fører til polynomet til lik null. Vi ønsker å finne ut hvilken faktor som gjør polynomet lik null når vi erstatte faktor for hver "x" i ligningen.
- La oss starte med å bruke vår første faktoren, en. La oss erstatte "1" for hver "x" i ligningen:
(1) 3 - 4 (1) 2 - 7 (1) + 10 = 0 - Dette gir oss: 1 - 4 - 7 + 10 = 0.
- Fordi 0 = 0 er et sant utsagn, vet vi at x = 1 er en løsning.
- La oss starte med å bruke vår første faktoren, en. La oss erstatte "1" for hver "x" i ligningen:
- 4Gjør litt ommøblering. Hvis x = 1, kan vi omorganisere uttalelse å se litt annerledes uten å endre hva det betyr.
- "X = 1" er det samme som "x - 1 = 0" eller "(x - 1)". Vi har nettopp trukket en "1" fra hver side av ligningen.
- 5Faktor rot ut av resten av ligningen. "(X - 1)" er vårt rot. La oss se om vi kan faktor det ut av resten av ligningen. La oss ta det ett polynom gangen.
- Kan vi faktor (x - 1) ut av x 3? Nei, vi kan ikke. Være vi kan låne en-x 2 fra den andre variable, så vi kan faktor det: x 2 (x - 1) = x 3 - x 2.
- Kan vi faktor (x - 1) ut av hva som gjenstår fra vår andre variable? Nei, igjen, vi kan ikke. Vi trenger å låne en annen liten bit fra den tredje variabelen. Vi trenger å låne en 3x fra-7x. Dette gir oss-3x (x - 1) =-3x 2 + 3x.
- Siden vi tok en 3x fra-7x, er vår tredje variabel nå-10x og vår stadige er 10. Kan vi faktor dette? Vi kan! -10 (X - 1) =-10x + 10.
- Det vi gjorde var å omorganisere variabler slik at vi kan faktor ut en (x - 1) ut av hele ligningen. Vår omarrangert ligning ser slik ut: x 3 - x 2 - 3x 2 + 3x - 10x + 10 = 0, men det er fortsatt det samme som x 3 - 4x 2 - 7x + 10 = 0.
- 6Fortsett å substituere med de faktorer av den frie sikt. Se på tallene som vi priset ut med (x - 1) i trinn 5:
- x 2 (x - 1) - 3x (x - 1) - 10 (x - 1) = 0. Vi kan omorganisere dette å være mye enklere å faktor en gang: (x - 1) (x 2 - 3x - 10) = 0.
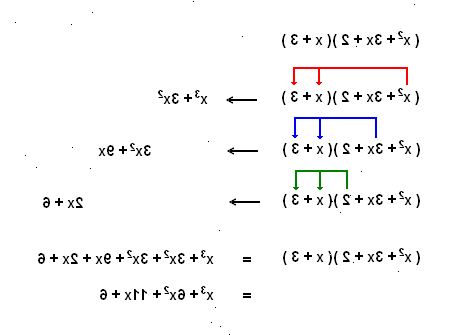
- Vi prøver bare å faktor (x 2 - 3x - 10) her. Disse faktorer ned i (x + 2) (x - 5).
- 7Dine løsninger vil være priset røtter. Du kan sjekke om dine løsninger faktisk fungerer ved å koble hver enkelt, individuelt, tilbake til den opprinnelige ligningen.
- (X - 1) (x + 2) (x - 5) = 0 Dette gir oss løsninger av 1, -2, og fem.
- Plug -2 tilbake i ligningen: (-2) 3-4 (-2) 2 - 7 (-2) + 10 = -8 til 16 + 14 + 10 = 0.
- Hane 5 tilbake inn i ligningen: (5) 3 - 4 (5) 2-7 (5) + 10 = 125 - 100 - 35 + 10 = 0.
Tips
- Den kubiske polynom er et produkt av tre første-graders polynomer eller et produkt av en første-graders polynom og annen unfactorable annengrads polynom. I dette siste tilfellet bruker vi lang divisjon etter å finne den første polynomet å få annengrads polynom.
- Det er ingen unfactorable kubikk polynomer enn de reelle tallene fordi hver kubikk må ha en reell rot. Cubics som x ^ 3 + x + 1 som har en irrasjonell virkelige roten kan ikke være priset inn polynomer med heltall eller rasjonelle koeffisienter. Selv om det kan være tatt med den kubiske formel, er det som et heltall ureduserbart polynom.
