Når rette linjer skjærer hverandre på et to-dimensjonalt diagram, møter de ved bare ett punkt, som kan beskrives ved et enkelt sett med x-og y-koordinater. Fordi begge linjene går gjennom det punktet, du vet at x-og y-koordinatene må tilfredsstille både ligninger og, så lenge du arbeider med rette linjer, vet dere er de de eneste koordinater som er gyldige i begge likningene. I stedet for å prøve å gjette skjæringspunktet ved å myser på en graf, kan du bruke grunnleggende algebraiske teknikker for å få et eksakt svar.
Trinn
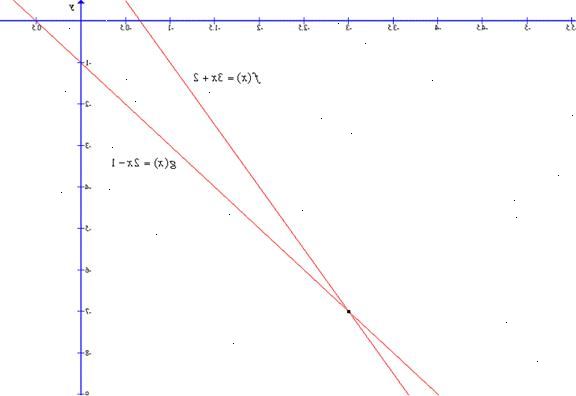
- 1Skriv ligningen for hver linje med y alene på venstre side av likhetstegnet, og x og alle andre koeffisienter eller konstanter på den andre siden av likhetstegnet.
- Det er ingenting galt med å skrive y på høyre side av likhetstegnet i stedet, men å ha den på venstre er den aksepterte konvensjonen.
- Noen ganger kan du se linjen notert som en funksjon i form av x, vil du se et symbol som f (x) eller g (x), etterfulgt av en eller flere betingelser med variabelen x. (I sjeldne tilfeller kan du se konstanter bare, uten variabelen x.) I dette tilfellet bare erstatte f (x) eller g (x) med "y".
- 2Sett på høyre side av hver ligning er lik den høyre siden av den andre ligning, løse med hensyn på x. Så hvis dine to ligninger var y = x + 3 og y = 12 - 2x, du ville ha x + 3 = 12 - 2x.
- Utføre grunnleggende algebraiske operasjoner som er nødvendige for å isolere den variable periode på en side av ligningen. Du kan utføre noen operasjon så lenge du gjør det til begge sider av ligningen. I dette tilfelle legger 2x til begge sider av ligningen gir 3x + 3 = 12. Ved å trekke fra 3 fra begge sider av ligningen gir 3x = 9, og endelig dividere begge sider av tre gir x = 3.
- Den resulterende x verdien er halvparten av koordinatpar for hvor de to linjene krysser hverandre. Nå må du finne y-verdien til skjæringspunktet.
- 3Plugg x-verdien du nettopp oppdaget i enten ligningen, og løse for y.
- I dette tilfellet, plugging x = 3 i den første ligningen gir y = 3 + 3, som forenkles til y = 6.
- Sjekk ditt arbeid ved å koble x-verdien inn i den andre ligningen, bør du få det samme svaret. I dette tilfellet har vi y = 12 - 2 (3), som forenkles til y = 12-6 eller y = 6. Så arbeidet sjekker.
- 4Legg den resulterende y-verdi til koordinatpar for skjæringspunktet. Du har nå både koordinater. Koordinatpar er vanligvis gitt i parentes, og x-verdien er alltid oppført først. Å fullføre eksemplet er svaret (3,6).
