Determinanter av matriser er meget nyttige og nødvendige for å finne den inverse av en matrise for hånd, så vel som for å bruke visse ligning løse prosesser som Cramer regel. Også, hvis determinanten er 0, vet du ligningene som utgjør matrise er lineært avhengige.
Trinn
- 1La M være 3x3 matrise og dens determinant vil være | m |.
Eksempel:en 11 et 12 en 13 1 5 3 M = en 21 en 22 en 23 = 2 4 7 en 31 en 32 en 33 4 6 2 - 2Ta en referanse rad eller kolonne. Tar en referanse rad eller kolonne i dette problemet er et viktig skritt som om du velger med omhu, så kan du lette problemet veldig mye og løse problemet i svært mindre tid.
- Vanligvis første rad er tatt som referanse. Hvis den gitte matrisen har null i sine elementer, og deretter velger referansen rad eller kolonne, som har de fleste nuller.
- Det er et tegn konvensjon for referanse rad eller kolonne som sier at du trenger å gjøre beregningen. Legg merke til at dette skiltet konvensjonen kun for referanse rad eller kolonne. Skiltet konvensjonen er gitt nedenfor.
(+) A 11 (-) A 12 (+) A 13 M = (-) A 21 (+) A 22 (-) A 23 (+) A 31 (-) A 32 (+) A 33
- Vanligvis første rad er tatt som referanse. Hvis den gitte matrisen har null i sine elementer, og deretter velger referansen rad eller kolonne, som har de fleste nuller.
- 3Velg det første elementet fra referansen rad eller kolonne, og kryss ut andre elementer fra rad og kolonne er valgt element i.
- Beregn determinanten av 2X2 matrise som er igjen etter å ha krysset ut elementer i trinnet ovenfor. Deretter multiplisere 2X2 determinant med utvalgte referanse element og tilsvarende skilt for at referansen element.
- Hvis du tar første rad som referanse, så for det første elementet:
(+) En 11 * ((en 22 * a 33) - (en 23 * 32)) = 1 (4 * 2 - 7 * 6) = -34
- Beregn determinanten av 2X2 matrise som er igjen etter å ha krysset ut elementer i trinnet ovenfor. Deretter multiplisere 2X2 determinant med utvalgte referanse element og tilsvarende skilt for at referansen element.
- 4Velg det andre elementet fra referansen rad eller kolonne, og kryss ut andre elementer fra rad og kolonne er valgt element i.
- Beregn determinanten av 2X2 matrise som er igjen etter å ha krysset ut elementer i trinnet ovenfor. Deretter multiplisere 2X2 determinant med utvalgte referanse element og tilsvarende skilt for at referansen element.
- Hvis du tar første rad som referanse, så for de andre element:
(-) Av en 12 * ((en 21 * a 33) - (a 23 * a 31)) = (-) 5 (2 * 2-7 * 4) = 120
- Beregn determinanten av 2X2 matrise som er igjen etter å ha krysset ut elementer i trinnet ovenfor. Deretter multiplisere 2X2 determinant med utvalgte referanse element og tilsvarende skilt for at referansen element.
- 5Velg det tredje elementet fra referansen rad eller kolonne, og kryss ut andre elementer fra rad og kolonne er valgt element i.
- Beregn determinanten av 2X2 matrise som er igjen etter å ha krysset ut elementer i trinnet ovenfor. Deretter multiplisere 2X2 determinant med utvalgte referanse element og tilsvarende skilt for at referansen element.
- Hvis du tar første rad som referanse, så for tredje element:
(+) En 13 * ((en 21 * 32) - (en 22 * a 31)) = 3 (2 * 6 - 4 * 4) = -12
- Beregn determinanten av 2X2 matrise som er igjen etter å ha krysset ut elementer i trinnet ovenfor. Deretter multiplisere 2X2 determinant med utvalgte referanse element og tilsvarende skilt for at referansen element.
- 6Legg resultatene for tre elementer av referansen rad eller kolonne for å få determinant av at 3x3-matrise.
| M | = -34 + 120 - 12 = 74
Tips
- Dersom alle elementene i en rad eller kolonne i en matrise, er null, så determinant av nevnte artikkel er også null.
- Hvis du tar første rad som referanse, så determinant vil være:
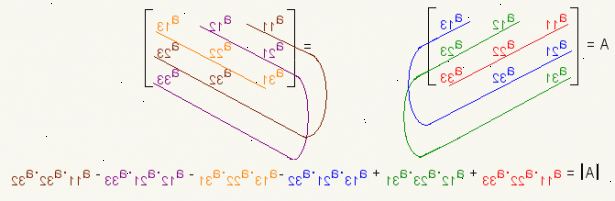
| M | = a 11 * ((en 22 * a 33) - (en 23 * 32)) - en 12 * ((en 21 * a 33) - (en 23 * a 31)) + en 13 * ( (en 21 * 32) - (en 22 * a 31)) - Denne metoden strekker seg til kvadratiske matriser av alle størrelser.
Advarsler
- Prøv å unngå å gjøre determinanter av noe større enn en 3x3 for hånd.
