Hvordan beregne Laplace transform av en funksjon

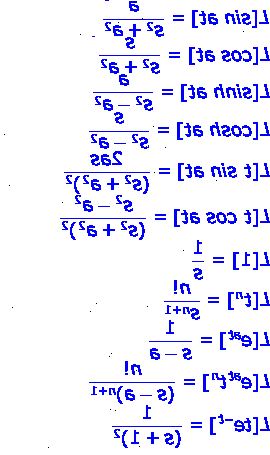
1. 1
   Vite om du prøver å finne den ensidige (ensidig) Laplacetransformasjonen eller bilaterale (tosidige) Laplace transform av funksjonen. Hvis typen Laplace transform ikke er angitt, kan det antas at du bør beregne ensidig versjon.
   • En ensidig Laplace transform er definert som:
   • En bilateral Laplace transform er definert som:
2. 2
   Sett funksjon, f (t), inn i definisjonen av Laplace transform.

Terminologi

1. 1
   Betrakt "Laplacetransformasjoner" - Det er dels et system for å konvertere tidsavhengige relasjoner domene til et sett med ligninger uttrykt i form av Laplace-operatoren 's'. Deretter blir oppløsningen av det opprinnelige problem utføres ved "kompleks-algebra manipulasjoner" i 's' eller Laplace-domenet og ikke i tidsdomenet:
   • "Bruk Laplacetransformasjoner er analogt til å bruke logaritmer å forenkle visse typer matematiske operasjoner. Ved å ta logaritmer, er tallene forvandlet til krefter av 10 eller e (naturlige logaritmer). Som et resultat av de transformasjoner, er matematiske multiplikasjon og divisjoner erstattet av tilleggene og subtractions hhv. "
2. 2
   "Tilsvarende gjelder Laplacetransformasjoner til analyse av systemer som kan beskrives av lineære, ordinære tid differensialligninger overvinner noe av kompleksiteten som oppstår i tiden-domain løsning av slike likninger.", Og, også:
   • Laplace Transform innebærer å integrere fra 0 til uendelig av gangen variabel f (t) fremkommer ved å multiplisere f (t) av ^e-st.
   • f (t) er brukt funksjon som må være definert for alle positive verdier av t.
   • s er en kompleks algebra variabel definert ved: s = a + jω der j = sqrt (-1), så du vil være delvis ved hjelp av imaginære tall.
     • Symbolet i (j i elektroteknikk) brukes til å representere √ -1. Derfor, for eksempel, √ (-4) = 2i. Antallet jeg ringte, eller 1i, eller xi kalles rent imaginære tall.
   • En bruk av den komplekse planet er kjent som s-planet. Den brukes til å visualisere røttene av ligningen som beskriver et system atferd (den karakteristiske ligningen) grafisk. Ligningen blir vanligvis uttrykt som et polynom i parameteren 's' av Laplace transform, derav navnet 's' fly.
     • Komplekse plan ved hjelp Argand diagrammene viser Z-planet, hvor z = x + iy og kan bruke z-Transformeringer samt Laplace. I matematikk og signalbehandling, konverterer Z-transform en diskret tids-domene-signal, som er en sekvens av reelle eller komplekse tall, til en kompleks frekvens-domene representasjon. Den kan betraktes som en diskret tid ekvivalent av Laplacetransformen. Denne likheten er utforsket i teorien om tidsskala beregning. Ved bilineær transformasjon, komplekset s-planet (Laplace av transform) kartlagt til det komplekse z-planet (i Z-transform).
       • Z = a + ib, = re ^ itheta, a = reell del av z, b = imaginære delen av z, r = modulus av z, theta = argument for z, a & b er reelle tall. Selv om denne kartleggingen er (nødvendigvis) -lineær, er det nyttig ved at den kartlegger hele jΩ aksen av s-planet på enhetssirkelen i z-planet, dvs. at jΩ aksen er i området ved konvergens av Laplacetransformen.

Løse transformeringen

1. 1
   Gjennomføre integrasjonen med integrering av deler. Avhengig av funksjon din, f (t) du trenger for å gjennomføre integreringen av deler flere ganger for å fullt ut integrere integrert.
2. 2
   Sette grensene i følge din. Skriv ut ligningen erstatte t med uendelig deretter skrive ut den negative av den samme ligning, denne gang erstatte t med 0. Forenkle dette ned så mye du kan, huske følgende verdier:
3. 3
   Sjekk svaret ved hjelp av en tabell over Laplacetransformasjoner.

Usammenhengende funksjoner

En usammenhengende funksjon kan skrives som:

hvor c er en konstant, og A og B kan være enten konstanter eller funksjoner av T. Mens dette eksempelet har bare to deler, kan det være noen endelig antall.

1. 1
   Skriv ut summen av Laplacetransformasjoner av hver del av usammenhengende funksjonen og bruk angitte grensene, i stedet for den vanlige 0 til ∞.
2. 2
   Beregn Laplacetransformasjoner som vist ovenfor. Husk å erstatte i de riktige grenser, snarere enn 0 og ∞.
3. 3
   Forenkle resultatet så mye som mulig.

Ved hjelp av egenskapene til Laplacetransformasjoner

1. 1
   Forsøke å utlede en Laplace transform av en funksjon, hvis det ligner en eller flere andre funksjoner, som du vet transform av. For eksempel:
   • Den Laplacetransformen av en lineær kombinasjon av funksjoner er de samme lineær kombinasjon av Laplacetransformasjoner.
   • Den Laplacetransformen av tf (t) er lik-F '(r), der F (s) er Laplace-transformerte av f (t) og f' (e) er dens derivat (proof).
   • Den Laplacetransformen av f '(t) er lik sF (S)-f (0).
   • Den Laplacetransformen av e ^ (at) f (t) er lik f (SA).
   • Den Laplacetransformen av en konvolu-sjon mellom to funksjoner f og g er lik produktet av deres Laplacetransformasjoner.
2. 2
   Bruk forskjellige kjente egenskapene til Laplacetransformasjoner å kunne utlede dem ved hjelp av trinnene ovenfor. Det er også nyttig å vite meningen bak hver eiendom.
3. 3
   Undersøke denne forenklede generell uttalelse, "Laplace transform av f (t) er lik funksjon F av s" og skriv: Laplace {f (t)} = F (s)
   • Tilsvarende gjelder den Laplace-transformerte av en funksjon g (t) skrives: laplace {g (t)} = G (s)