Hvordan graf poeng på koordinatplan

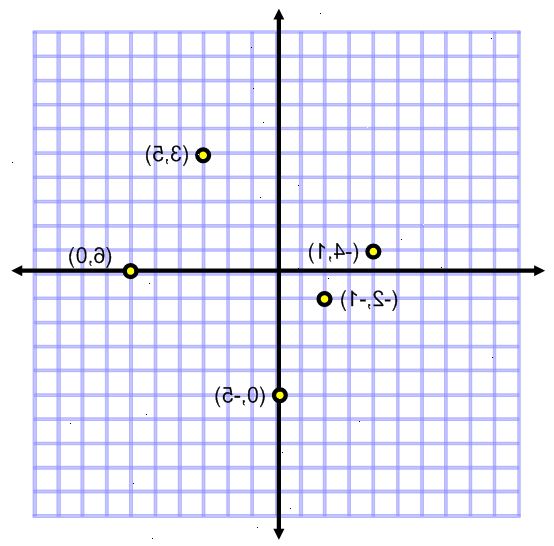
For ett poeng

1. 1
   Finn den første koordinat i et ordnet par er på x-aksen.
   • X-aksen går til venstre og høyre, er den andre koordinat på Y-aksen.
   • Y-aksen går opp og ned.
   • Positive tall går opp eller rett (avhengig av aksen). Negative tall gå til venstre eller ned.
2. 2
   Bestem kvadrant poenget er in.
   • Husk at en graf har fire kvadranter (vanligvis merket i romertall). I kvadrant får (+, +); kvadrant I er ovenfor og til venstre for y-aksen. Kvadrant IV får (+, -); kvadrant IV er under x-aksen og til høyre for Y-aksen. (5,4) er i kvadrant I. (-5,4) er i kvadrant II. (-5, -4) Er i kvadrant III. (5, -4) er i kvadrant IV.
3. 3
   Marker punktet.

For grafer av linjer, sirkler, parabler etc.

1. 1
   Avgjør formen din grafen vil ta. Blir det en linje, parabel, sirkel, osv.
   • Denne delen vil ikke lære deg hvordan å tegne en linje, parabel, osv. Du bør vite at i klassen. Dette vil hjelpe deg til å endre grafen tilpasses situasjonen. Hvis du gjør disse grafene for første gang, graf dem ved hjelp av en rekke punkter.
   • Læreren din vil ikke være interessert i deg plotte presise punkter av disse typer grafer. Du lærer vil være interessert i om du vet hvordan du skal finne (og identifisere) disse punktene. Læreren din vil være på utkikk etter en graf av riktig form, kvadrant (s), orientering, helling, og at de viktige punktene er notert.
2. 2
   Bestemme hvilke punkter du skal ha med på grafen. Komplekse grafer krever flere poeng.
   • Med mindre du bare tegnes et punkt, vil du trenger minst to punkter. En linje krever to punkter. En sirkel krever to poeng hvis man er sentrum, tre hvis sentrum er ikke inkludert (Med mindre din instruktør har tatt sentrum av sirkelen i problemet ved å bruke tre). En parabel krever tre poeng, en å være det absolutte minimum eller maksimum, de andre to punktene bør være motsetninger. En hyperbel krever seks poeng, tre på hver akse.
3. 3
   Forstå hvordan å endre ligningen endres grafen.
   • Endre X-variabelen beveger ligningen til venstre eller høyre.
     Snu den negative (multiplisere med -1) knipser det over, hvis det er en linje, vil det endre den fra å gå opp til ned eller går ned og opp.
     
   • Betrakt ligningen y = x ^ 2, en parabel med sin base i (0,0).
     Y = (x-2) ^ 2 er den samme parabel, bortsett fra den tegnes to mellomrom til høyre for opprinnelsen; sin base er nå på (2,0).
     y =-x ^ 2 (den negative påføres etter at eksponent ^ 2) er en opp-ned y = x ^ 2; sin base er (0,0).
     y = 5x ^ 2 er fortsatt en parabel, men det blir større enda raskere, gir det en tynnere utseende.