Hvordan bruke Pythagoras 'læresetning

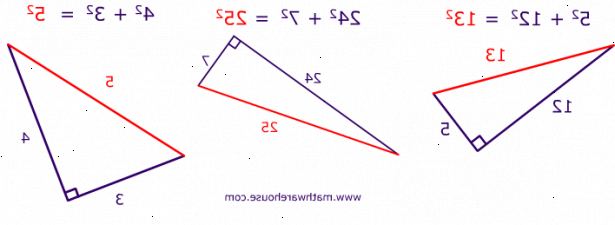
På rettvinklede trekanter

1. 1
   Skriv ut Pythagoras 'læresetning: a ² + b ² = c ², og tegne et bilde av trekanten du løse.
2. 2
   Merke tegningen din. Merke korteste sidene 'a' og 'b' (spiller ingen rolle hvilken side som er a eller b), og etiketten hypotenusen (den lengste siden, motsatt av den rette vinkelen) 'c'.
3. 3
   Bestem hvilken side av trekanten du løse for: a, b eller c. Vanligvis vil du bli gitt to av sidelengdene og bruke formelen til å løse for den tredje.
4. 4
   Skriv om ligningen med de kjente verdiene.
   • Hvis du får de to sidelengder (si 3 og 4), skriver:
     3 ² + 4 ² = c ²
   • Hvis du får den ene siden og hypotenusen (3 og 5), skriv:
     3 ² + b ² = 5 ²
5. 5
   Beregn rutene.
   • Det første eksempelet ovenfor bør omskrives: 9 + 16 = c ².
   • Den andre: 9 + b ² = 25.
6. 6
   Kombiner like vilkår.
   • I dette tilfellet alle vilkår på venstre side av ligningen er konstant, slik at vi kan legge dem til får: 25 = c ².
   • I det andre eksemplet må du trekke fra tre ² fra begge sider av ligningen for å isolere variabel.
7. 7
   Ta kvadratroten.
   • Etter å ta kvadratroten av begge sider av ligningen, er du igjen med:
     c = 5.

Eksempel: gitt at hypotenusen er 10, og det ene beinet er 8, finne lengden av det andre benet.

en ² + b ² = c ²

(8) ² + b ² = (10) ²

64 + b ² = 100

b ² = 100-64

b ² = 36

b = kvadratroten av 36

b = 6

Eksempel: En stige lener seg mot en bygning. I bunnen av stigen er 5 m fra bunnen av veggen. Stigen når 20 meter opp på veggen av bygningen. Hvor lenge er stigen?

"5 m fra bunnen av veggen" betyr en = 5
"Når 20 meter opp på veggen" betyr b = 20
stigen lengde er hypotenusen, så c er ukjent

en ² + b ² = c ²

(5) ² + (20) ² = c ²

25 + 400 = c ²

425 = c ²

c = kvadratroten av 425

c = 20,6 (avrundet til nærmeste tidel)

Så den omtrentlige lengden på stigen er 20,6 meter.

Som en del av avstanden formelen

Avstanden formel brukes i geometrien til å finne den rette linjen avstanden mellom hvilke som helst to punkter.

1. 1
   Bestem hva poeng å bruke. Typisk punkter er gitt som ordnede par.
2. 2
   Plotte punkter på en graf. (X, y) hvor x er den horisontale aksen, og y er vertikal.
3. 3
   Finn lengden av sidene i trekanten din. Du kan gjøre dette ved å telle forskjellen på grafen, eller ved å bruke (x ₁ - x ₂₎ for x, og (y ₁ - y ₂₎ for y.
4. 4
   Bruk Pythagoras 'læresetning. Avstanden mellom punktene er hypotenusen i trekanten.

Eksempel:
3-6 = -3 (x)
(-3) ² + (4) ² = c ²
c = sqrt (25)

På ikke-rettvinklede trekanter ved hjelp av trigonometri

Dette avsnittet bruker eksempelet av de to byene fra oven, i dette tilfellet må du løse for avstanden fra byen A til City C.
For dette eksempelet anta sider 'a' og 'b' er kjent (se tegning nedenfor).

1. 1
   Tegn et bilde av trekant din.
2. 2
   Tegn høyde. En høyde er en linje vinkelrett på hypotenusen som passerer gjennom den motsatte toppunktet. I dette tilfellet er høyden er 'c.'
3. 3
   Måle vinkelen mellom linje som forbinder byen A til B og høyde linje.
   
   • Vanligvis vinkelen vil bli gitt på denne typen problem. Hvis ikke, måle vinkelen ved hjelp av en vinkelmåler.
4. 4
   Bruk av trigonometrisk funksjon for å finne lengden på høyde:
   Hvis lengden "a" er kjent, og deretter: cos (A) = c / a og c = Acos (A)
5. 5
   Bruk Pythagoras 'læresetning for å finne lengden av linjen fra byen A til høyde:
   x1 = sqrt (a ² - c ²⁾
6. 6
   Bruk Pythagoras 'læresetning til å finne avstanden mellom høyde linje og byen C: x2 = sqrt (b ² - c ²⁾
7. 7
   Ta summen av x1 og x2.
8. 8
   Eksempel: Du bor i by A og har en venn som bor i byen C, og ønsker du å vite hvor langt din venn bor fra deg. Du vet det om en 50 mils kjøring til City B, deretter en annen 100 miles derfra til City C. Hvor lenge er en rett linje fra City A til by C? (Rund alle beregninger til nærmeste tiende)
   
   • Tegn høyde linjen og måle vinkelen.
     
   • Bruk cosinusfunksjon å finne lengden på høyde:
     lengde = 50 x cos (30) = 50 x 0,866 hvilke runder til 43,3 miles
   • Bruk Pythagoras 'læresetning for å finne lengden av x1:
     x1 = sqrt (50 ^{2 til} 43,3 ²⁾ = sqrt (625,11) = 25,0 miles
   • Bruk Pythagoras 'læresetning for å finne lengden på avstand x2:
     x2 = sqrt (100 ^{2 til} 43,3 ²⁾ = sqrt (8125,1) = 90,1 miles
   • Legg de to distanser sammen for å finne den totale distansen:
     

I vektor tillegg

Pythagoras teorem brukes når løse for resulterende vektorer. Dette gjøres ved å bryte vektorer i 'x' og 'y' komponenter (og "z" i 3d), og legge ut komponenter. De resulterende komponenter (sidene av rettvinklet trekant) kan brukes til å løse med hensyn på det erholdte (hypotenusen).

1. 1
   Bryte vektorer i x-og y-komponenter. Vektorer har retning og størrelse, og den retning er vinkelen opprettet mot urviseren fra den positive x-aksen, og omfanget er lengden til vektoren. Å bryte vektor i komponenter, vil du bruke trigonometri. For eksempel, en vektor med størrelse 'M' og vinkel '30 ':
   • x = M * cos (30)
   • y = M * sin (30)
2. 2
   Legg ut komponenter. Nå som vektorer er brutt i x-og y-komponenter, tar summen av x-komponentene og summen av y-komponenter. Dette er sidene i trekanten din.
3. 3
   Bruk Pythagoras 'læresetning. I dette tilfellet (summen av x) ² + (sum av y) ² = c ², hvor 'c' er den resulterende størrelsesorden.

Eksempel:
[10cos (30) + 15cos (45)] = 19,27 (avrundet til nærmeste hundredel) (x)
(19.27) ² + (15.61) ² = c ²
c = sqrt (615,005)