Hvem det var som sa du kunne få et nummer å si noe var helt rett. Det han ikke sa, var imidlertid hvor enormt terapeutiske det er å få dem til å si hva du vil. Så nyt den tilfredsstillende prosess med "beviser" matematisk at du virkelig gjøre 149 260€ / år, har en 10 000 kvadratmeter hjem, og er frisk som en fele ved å følge disse trinnene.
Trinn
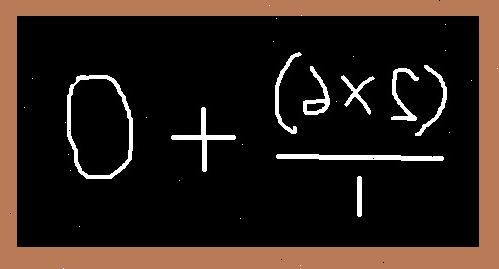
- 1Brette opp ermene. Dette oppnår mer enn bare den praktiske fordelen av å ikke få ermene skitne og flekkete med bly. Den lar tilskuerne vet at du er seriøs om matematisk bevise at du er virkelig en 6 '6 "person, bare forvrengt av lyset for å se ut som en 4' 3" person. Dessuten er det bra for å la dem vite at du ikke har noe opp ermene.
- 2Ta ut et ark med papir og Merk: Bruk alltid en ved ansettelse av algebraiske smutthull for ethvert formål Sub-Note:.. Selvfølgelig, har du sannsynligvis ikke trenger å slette noe, men dette vil vise seg å være fordi du brukte en; hvis du bruker en, vil du gjør en feil og vil ønske at du hadde bare brukt en blyant i første omgang.
- 3Skriv på toppen av papiret det virkelige antall og den "virkelige" nummer. I eksemplet vil dette være tre baller og 11 baller for å vise at den personen som tre baller er egentlig 11.
- 4Skriv 'gitt a = b' på en ny linje.
- 5Utfør følgende matematiske operasjoner:
3a = 3b (Multiplisere begge sider av det reelle tallet) 11a = 11b (Multiplisere begge sider av den "ekte" nummer) 3a 2 = 3ab (Multiplisere med en på begge sider) 11AB = 11b 2 (Multiplisere med b på begge sider) 3a 2 - 11AB = 3ab - 11b 2 (Trekke det over to ligninger for å gjøre en) 3a 2 - 3ab = 11AB - 11b 2 (Trekke 3ab og legge 11AB til begge sider) 3a 2 - 3ab + ab - b 2 = 12AB - 12b 2 (Legge ab og trekke b 2 fra begge sider) 3a (ab) + b (ab) = 12b (ab) (Factoring ut felles faktorer) 3a + b = 12b (Fjerning av felles faktorer * Advarsel: dette trinnet deler med 0, er som algebraically udefinert og derfor holder ikke sant i et bevis) 3a = 11b (Trekke b fra begge sider) 3b = 11b (Erstatte en for b, huske at de er like) 3 = 11 (Fjerning av vanlige vilkår) - 6Tegn opp en liten kvadrat på slutten av den siste linjen, og fyll det ut. Til en matematiker, betyr dette "darn tootin '" eller "case closed" eller "quod erat demonstrandum" eller "denne logikken er så ugjendrivelige som Pied Piper rør etter at hans sønn kjørte over den med gressklipperen "(vel, egentlig, er at siste" irreflutable, "men det er nok riktig her allikevel).
- 7Sug i tilfredsstillelse av, for et øyeblikk, har den seks-tallet lønn og romslig sommeren hjemme, utrolig nok, i en alder av 23! (Wow, du ser flott ut!) Eller, selvfølgelig, tilfredsstillelse av å være en mester sjonglør, hvis det er det flyter båten.
Tips
- Spoiler! ikke les hvis du ønsker å finne ut selv hvorfor dette ikke fungerer egentlig dette beviset jakter på en interessant matematisk nei-nei, skjult i algebra av beviset! med null. Legg merke til at vi bestemte oss i begynnelsen at a = b. Så, når vi faktor ut ab, er vi faktisk dele alle vilkår av ab å gjøre det. Vel, er ab 0 siden a og b er like, og divisjon med 0 er ulovlig. (Sneaky matematikere...) Uansett, det er mange varianter av disse smutthull som, mens de kan vises algebraically lyd, er de i virkeligheten falsk. Prøv skjule kvadratroten av et negativt i en variabel eller en imaginær. Hvilke andre ting kan du "bevise"?
- Det finnes utallige som ville være bedre hvis de var bare noe annerledes, alder, GPA, kredittkort nummer, det beløpet du skylder kredittkortselskapet, og hvor mange ganger du har vært sent til denne uken, bare for å nevne noen.
- Hvis du føler deg spesielt nerdete, kan du prøve å bevise at π = 3, eller som e = 2. Nå, som ville virkelig forenkling π liv!
- Nøye vurdere konsekvensene av beviset ovenfor, er det noen problemer med det? Les videre, hvis du ønsker å vite...
