Hvordan finne arealet av en firkant

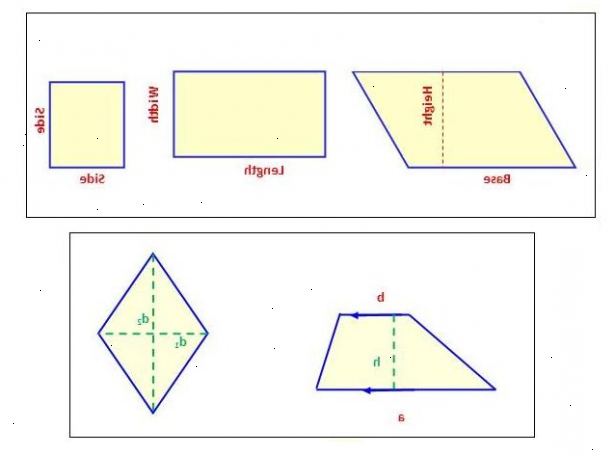
Kvadrater, rektangler og andre parallellogrammer

1. 1
   Vite hva et parallellogram er. Et parallellogram er enhver firkant med to par av parallelle sider, som i den motsatte eller motstående sider er like lange. Firkanter, rektangler og rhombuses er alle parallellogrammer.
   
2. 2
   Finne arealet av et kvadrat. Fordi hver side av et kvadrat er like lange, vil du ganske enkelt kvadrat lengden på den ene siden, kalt t. Bruk følgende ligning:
   
   • K = t ²
3. 3
   Finne arealet av et rektangel. For å finne arealet av et rektangel, trenger du to mål: bredde, eller base (den lengste siden av rektangelet), og lengden, eller høyde (den korteste siden av rektangelet). Formelen er:
   
   • K = b * h
4. 4
   Finn arealet av en rombe (eller diamant). For å finne arealet av en rombe, må du vite høyden, som er definert som den vinkelrette avstanden mellom to parallelle sider. Vær forsiktig med dette - du kan ikke bare multiplisere den ene siden av en tilstøtende side. Hvis du trenger å finne høyden på et parallellogram, prøve å tegne linjen for høyden slik at du har en trekant med en 90-graders vinkel. Når du har skaffet høyden, bruker du denne formelen:
   
   • K = b * h

Finne arealet av en trapes

1. 1
   Vet hva en trapes er. En trapes er en firkant med minst to sider som går parallelt med hverandre. Hver av de fire sider på et trapes kan være en annen lengde. Det er to forskjellige måter du kan finne arealet av et trapes, avhengig av hva slags informasjon du har.
   
2. 2
   Finn høyden av trapesform. Høyden på en trapes er vinkelrett linje fra toppen grunnlag, og den nederste grunnlinjen, og du trenger det for både området ligninger. Dette vil ikke ha samme lengde som en av sidene, fordi hver side er rettet diagonalt. Her er hvordan du kan finne høyden:
   
   • Finn den kortere basen. Plasser blyanten ved hjørnet mellom den grunnlinje og en av sidene, og trekke en linje rett opp eller ned til den andre grunnlinjen. Du bør ha opprettet en trekant med en 90-graders vinkel.
   • Bruk trigonometri for å bestemme høyden. For eksempel, hvis du vet lengden på siden og at det er en 90-graders vinkel i trekanten, kan du anta at cosinus til 90 grader vil være lik høyden delt på lengden på siden.
3. 3
   Finn arealet av trapesens hjelp av høyden. Hvis man vet høyden av trapes, så vel som lengden av begge baser, bruk av følgende ligning:
   
   • K = (a + b) / 2 * h
4. 4
   Finn arealet av en trapes bruker midsegment. Den midsegment ville være en linje som går parallelt med bunnen og toppen linjer av trapezoid, og bør være en lengde som er nøyaktig mellom dem. Her er hvordan du arbeider med en midsegment:
   
   • Finn midsegment. For å bestemme midsegment m, ta gjennomsnittet av sidene a og b (eller topp og bunn "baser" av trapes). Bruk denne formelen: m = (a + b) / 2. Nå som du vet midsegment, kan du multiplisere det med høyden for å finne arealet. Bruk følgende ligning:
   • K = m * h

Finne arealet av en kite

1. 1
   Vet hva en kite er. En kite er definert som en geometrisk form som to par med samme lengde sider er ved siden av hverandre, som likner en real-life kite. Det er to forskjellige måter å finne området, avhengig av hva slags informasjon du har.
   
2. 2
   Finn den er av en kite med måling av sidene. Hvis du kjenner lengdene av to forskjellige sider, så vel som vinkelen i hjørnet mellom disse sider, bruke formelen hvori er vinkelen theta (θ):
   
   • K = (a * b) * sinθ
3. 3
   Finn arealet av en kite med diagonaler. En diagonal er den rette linjen mellom to motstående vinkler på kite. Hver kite har to diagonaler.
   
   • Bestemme lengden av en diagonal. Trekke en linje fra den ene side av dragen til en annen. Du skal nå ha to trekanter. Ved hjelp av, bestemmer lengden av diagonalen. (Husk at alle tre vinkler i en trekant må legge opp til 180 grader.)
   • Når du har funnet ut det første diagonal, bruker de samme prinsippene for å bestemme lengden av den andre. Deretter bruker denne ligning for å bestemme området, hvori p og q er hele lengdene av diagonalene:
   • K = (p * q) / 2

Ved hjelp av en generell ligning

1. 1
   Bruk en generell firkant område ligningen. Det finnes formler du kan bruke til å regne ut arealet av en firkant, uavhengig av sin form. Her er den mest vanlige, som bruker prinsippene om trigonometri:
   
   • Hvis K er det totale arealet av firkanten, a, b, c og d er lengdene av de fire sidene, A er vinkelen (i grader) mellom sidene A og D, og C er den vinkel (i grader) mellom sidene b og c, og deretter:
     • K = (0,5 * d) * sin A + (0.5b * c) * sin C
     • Hvis du prøver å finne arealet av et parallellogram, der de motsatte vinkler er like, reduserer ligningen til K = 0,5 (ad + bc) * sin A.