Skrive matematiske bevis kan være den vanskeligste delen av geometri, men de er essensielle. Hver geometri boken har et prøvetrykk delen, og kongruente trekant bevis tar opp en stor del. Siden prosessen kan avhenge av trekanter og din Givens, du sjelden følger nøyaktig den samme prosessen, noe som kan bli veldig frustrerende. Men det er et generelt mønster, og å følge disse retningslinjene vil hjelpe.
Trinn
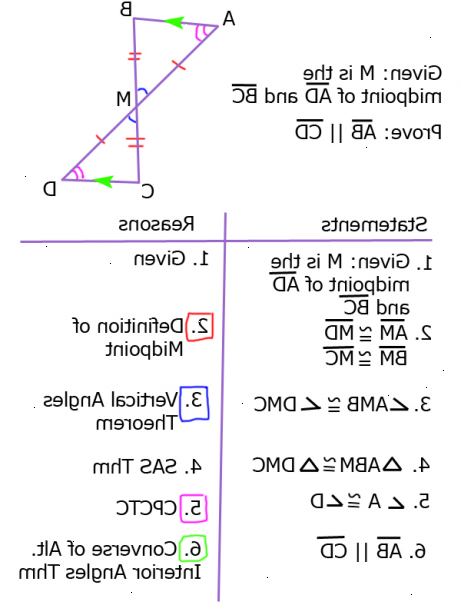
- 1Sett opp en to-kolonne bevis format. Den venstre kolonnen skal være merket "Uttalelser" og høyre kolonne merket "grunner".
- 2Kopier diagram på papir, spesielt hvis læreren krever at du gjør det.
- 3Listen din Givens som første skritt i din uttalelser kolonnen. Under grunner kolonnen, bør du skrive "gitt".
- 4Oversette givens til nyttig informasjon. For hver gitt, vil du ønsker å tenke hva du kan gjøre med denne kunnskapen. På dette punktet i beviset, vil de fleste av dine grunner være definisjoner.
- Hvis en av Givens er "Point C er midtpunktet av AB", ville kontoutskriften lese "AC = CB" og grunn ville være "Definisjon av midtpunkt".
- Hvis segment XY halverer segment NM, og P er det punktet hvor XY skjærer NM, ville kontoutskriften lese "NP = PM" og din grunn ville være "Definisjon av bisector".
- Hvis givens si "KL er vinkelrett på HJ", ville kontoutskriften være "Angle KLH er en rett vinkel". Bokstavene vil avhenge av diagrammet, som er en av grunnene til diagrammet er viktig.
- 5Se etter eventuelle likebente trekanter i diagrammet basert på Givens. Likebente trekanter er trekanter som har to ben med samme lengde. Skriv de to bena er sammenfallende som en uttalelse siterer "Definisjon av isosceles" som årsak.
- 6Se etter parallelle linjer. Hvis en tredje linje går gjennom dem begge, vil det danne alternative interiør vinkler og tilsvarende vinkler. Dette er ganske vanlig i trekant bevis. Den generelle formen som dannes av vinklene ser ut som en bokstaven "Z".
- Skriv inn din uttalelser kolonne som disse vinkler er kongruente til hverandre med årsaken å være "Alternative indre vinklene er kongruente" eller "Tilsvarende vinkler er kongruente".
- Ikke bruk årsaker som for eksempel "Definisjon av parallell" eller "Definisjon av alternative interiør vinkler". Disse er ikke gyldige bevis grunner.
- 7Se i diagrammet for vertikale vinkler. Vertikale vinkler vil danne en X og er de vinkler på tvers av hverandre, berører i midten, men ikke langs deres sider. Disse vertikale vinkler er kongruente. Et eksempel kan være å bruke utsagnet "Angle P er sammenfallende å vinkle R" med grunn "Vertical vinkler er kongruente".
- 8Se i diagrammet for noen linjer eller vinkler som deles av trekanter. Det er der den refleksive eiendom kommer inn i bildet.
- Kontoutskriften bør lese "XY = XY" eller "Angle A = vinkel A" og grunnen ville være "refleksiv eiendom kongruens".
- 9Overfør hver congruency setningen du har funnet så langt, inkludert Givens, inn i diagrammet. Kongruente sider blir merket med hash merker; kongruente vinkler er merket med buer.
- 10Se på en av trekantene i bildet. Legg merke all merking du nettopp laget, og de som ble gitt til deg. Hvor mange vinkler er kongruente? Hvor mange sider? Matche denne informasjonen med en av trekanten congruency teoremer. Kontoutskriften bør lese "Trekant ABC er kongruent til trekant XYZ" og grunn ville være det riktige valget mellom AAS, ASA, SAS, SSS, HL, etc.
- SSS står for side, side, side. Alle tre sider må være sammenfallende.
- To sider og en vinkel må være sammenfallende for det å være SAS (side, vinkel, side).
- Se om dine trekanter har kongruente rette vinkler, og to kongruente sider, en å være hypotenusen (som er den siden rett over fra den rette vinkelen). Hvis de gjør det, så si dem som sammenfallende med årsaken HL (Hypotenuse Leg Theorem).
- Det kan være ASA eller AAS hvis to vinkler er kongruente, men bare den ene siden.
- 11Ta en titt på "bevise"-linjen til problemet ditt. Hvis det er det samme som ditt siste utsagn, så er du ferdig.
Tips
- Hvis diagrammet ikke har to trekanter, så du kan ha en annen form for bevis. Dobbeltsjekk for å kontrollere at problemet ber deg om å bevise congruency av to trekanter.
- Hvis diagrammet har to overlappende trekanter, prøv redrawing dem som separate trekanter. Det vil være mye enklere å finne og markere de kongruente deler.
Advarsler
- Hvis givens inkludere ordet "vinkelrett," ikke si at en vinkel er 90 grader på grunn av definisjonen av loddrette linjer. I stedet skriver en uttalelse som sier slikt vinkel er en rett vinkel på grunn av "definisjon av loddrette linjer og deretter skrive en uttalelse som sier sa vinkelen er 90 grader på grunn av" definisjon av rett vinkel ".
- Du kan ikke bevise et teorem med seg selv. Hvis du prøver å bevise at basen vinkler er kongruente, vil du ikke kunne bruke "Base vinkler er kongruente" som en grunn til hvor som helst i beviset ditt.
