Slik finne overflatearealet av prismer

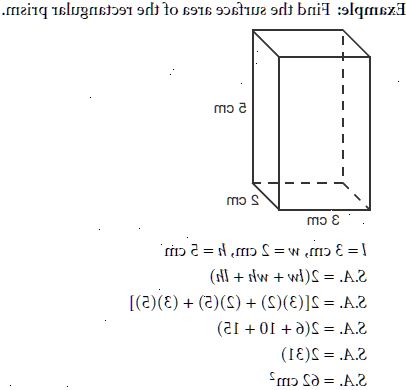
1. 1
   Etiketten så mange sider som du kan. Det fine med prismer er at de matchende end parene gjør det enkelt å bestemme mye av de enkelte målinger uten å måtte løse for noe. Enhver måling som er gitt for en av slutten figurer (f. eks høyde av trekanten, radien til sirkelen), gjelder også den tilsvarende form i den andre enden. Videre, hvis du vet lengden på den ene siden av prisme, vet du lengden på alle sidene. Distribuere disse tallene som er nødvendig rundt prisme for å se hva du har å jobbe med.

Finn arealet av en av de samsvarende ender

1. 1
   Hvis de samsvarende endene er trekanter, finne arealet av en trekant med.
2. 2
   Hvis de samsvarende endene er kvadratisk eller rektangulær, multiplisere basen etter høyde. Basen og høyde er bare de målinger av to vinkelrette sider av kvadrat eller rektangel, for en firkantet, disse to målinger er de samme. Bare multiplisere begge numre sammen for å finne området av enden.
3. 3
   Hvis de samsvarende endene er sirkler, multiplisere pi ved radius kvadrat. Radien er lengden fra sentrum av sirkelen til den ytre kanten. Kvadrere dette nummeret (dvs. multiplisere det av seg selv) og deretter multiplisere resultatet med pi (3,14159...). Dette gir deg området på slutten.
   • Hvis du har fått diameter (dvs. lengden på tvers av hele sirkelen), dividere dette tallet i to for å finne radius.
   • Hvis du har fått omkretsen (dvs. lengden på ytterkanten av sirkelen), dividere dette tallet med pi og dele det resultat av to til å finne radius.
4. 4
   Hvis de samsvarende endene er parallellogrammer, multiplisere basen etter høyde. Parallellogrammer er skjeve firkanter (som åpne bokser som har blitt skjøvet til side), de har to par parallelle sider, men ingen av hjørnene er rette vinkler. Bunnen av et parallellogram er simpelthen lengden av en av de to lange og dårlig tilpassede sider, hvor høyde, er imidlertid avstanden mellom disse to sider, ikke lengden av en av de skråstilte sider. Hvis denne høyden ikke allerede er gitt til deg, vil problemet be deg om å løse for det ved å slå på de vinklede sidene i en rettvinklet trekant og gir deg lengden på to av sidene i trekanten. Å løse for høyden på denne måten:
   • Bruke Pythagoras teorem, som er A ^ 2 + b ^ 2 = c ^ 2. Hypotenusen i trekanten, eller C, er ganske enkelt den side av trekanten på motsatt side av den rette vinkelen. Vi kaller den andre siden som er blitt gitt B C,>. For å løse for høyden, som vi kaller A, omorganisere formelen til A ^ 2 = C ^ 2 - B ^ 2. Multipliser C av seg selv, deretter multiplisere B av seg selv. Trekk fra det andre resultatet fra den første til å få A ^ 2, for å deretter løse for A, finne kvadratroten av denne summen. Dette er høyden av den parallellogram, som kan nå multiplisere med basen for å finne den totale areal.
5. 5
   Hvis de samsvarende ender er et annet polygon, bryte formen ned i trekanter å løse. En pentagon, for eksempel, kan bli brutt ned i fem like store trekanter, en sekskant kan deles inn i seks, og så videre. Når du er ferdig med å tegne trekanter, løse for området av en trekant med. Når du er ferdig, multiplisere dette området med det totale antallet av like trekanter du har tegnet.
   • Hvis mangekanten ikke kan brytes ned til perfekte trekanter, bryte det ned i trekanter og firkanter. Finn arealet av hver figur individuelt ved formen guider ovenfor, og deretter legge dem sammen for å finne det totale arealet av polygonet.
6. 6
   Legg merke til området i denne enden på papiret og la den være alene nå. Du kommer tilbake til det senere.

Finn omkretsen av et av de samsvarende ender

1. 1
   Løs for eventuelle manglende sider. Etter å løse for området, kan du allerede vet lengden på hver side av formen på slutten av prismet. Hvis ikke, løse ved hjelp av en av følgende metoder:
   • Hvis de samsvarende endene er trekanter, løse for alle sider ved hjelp av Pythagoras 'læresetning. Pythagoras 'læresetning er A ^ 2 + b ^ 2 = C ^ 2: A og B er i bunnen og høyden av en rettvinklet trekant, og C er hypotenusen, som ganske enkelt er den siden som er motsatt av den rette vinkelen.
     • Hvis du har fått A og B, bruke formelen C ^ 2 = A ^ 2 + B ^ 2. Multipliser En av seg selv, multiplisere B av seg selv, og legge de to tallene sammen, dette gir deg C ^ 2. Å deretter finne løsning for C, bare finne kvadratroten av denne summen.
     • Hvis du har fått C og B: bruke formelen A ^ 2 = C ^ 2 - B ^ 2. Multipliser C av seg selv, multiplisere B av seg selv, og trekke det andre resultatet fra den første, dette gir deg A ^ 2. Å deretter løse for A, bare finne kvadratroten av denne summen.
     • Hvis du har fått C og A: bruke formelen B ^ 2 = C ^ 2 - A ^ 2. Multipliser C av seg selv, multiplisere En av seg selv, og trekke det andre resultatet fra den første, dette gir deg B ^ 2. Å deretter løse for B, bare finne kvadratroten av denne summen.
   • Hvis de samsvarende endene er sirkler, finne omkretsen. Formelen for omkrets er C = D x pi: C er omkretsen og D er diameteren. Hvis du har radius, bare multiplisere dette med 2 for å finne diameter.
   • Hvis de samsvarende ender er et annet polygon, bryte formen ned i trekanter og / eller firkanter som før og finne ytterkantene ved å løse for disse figurene enkeltvis. Bruk form guider ovenfor om nødvendig.
2. 2
   Marker omkretsen målinger på papiret. Du kan så bruke dem til å bestemme arealet av sidene av parallellogrammet.

Finn arealet av hver side

1. 1
   Legg merke til at lengden av prismet. Dette er avstanden mellom de to samsvarende ender av prismet. Ettersom endene av prismet er parallelle, vil denne avstand være ensartet i hele - selv om de samsvarende ender er begge vinklet. Dette betyr at hvis du vet lengden på den ene siden, vet du lengden på alle sidene.
2. 2
   Finn arealet av hver side. Hver side vil enten være et kvadrat / rektangel eller et parallellogram. Parallellogrammer er skjeve firkanter (som åpne bokser som har blitt skjøvet til side), de har to par parallelle sider, men ingen av hjørnene er rette vinkler.
   • For å finne arealet av et kvadrat / rektangel, multiplisere basen etter høyde. Basen og høyde er bare de målinger av to vinkelrette sider av kvadrat eller rektangel, for en firkantet, disse to målinger er de samme. Bare multiplisere begge numre sammen for å finne området av enden.
   • For å finne arealet av et parallellogram, multiplisere basen etter høyde. Legg merke til at bunnen av et parallellogram er ganske enkelt lengde av en av de to lange og dårlig tilpassede sidene, den høyde, er imidlertid avstanden mellom disse to sider, ikke lengden av en av de skråstilte sider. Hvis du bare vet lengden på den vinklede side, men ikke parallellogram sanne høyde, tegne en linje gjennom hver side av parallellogram, snu den til en perfekt kvadrat / rektangel med en trekant på hver ende. For å finne høyden med denne trekanten:
     • Bruke Pythagoras teorem, som er A ^ 2 + b ^ 2 = c ^ 2. Hypotenusen i trekanten, eller C, er ganske enkelt den side av trekanten på motsatt side av den rette vinkelen. Vi kaller den andre siden som er blitt gitt B C,>. For å løse for høyden, som vi kaller A, omorganisere formelen til A ^ 2 = C ^ 2 - B ^ 2. Multipliser C av seg selv, deretter multiplisere B av seg selv. Trekk fra det andre resultatet fra den første til å få A ^ 2, for å deretter løse for A, finne kvadratroten av denne summen. Dette er høyden av den parallellogram, som kan nå multiplisere med basen for å finne den totale areal.
   • Hvis prismet er sylindrisk, finne arealet av sidene ved å multiplisere periferi, hvilket du løst i foregående avsnitt, med den totale høyde. (Bilde sylinderen har et stykke papir pakket rundt, som, når den er pakket inn, danner en perfekt kvadrat eller rektangel. Omkretsen kan deretter bli tenkt på som den lengden av det stykke stykke papir, som kan løses ut som en hvilken som helst kvadrat ved multiplisere lengde ganger høyde.)

Finn det totale arealet

1. 1
   Multiplisere arealet av enden av prismet ved to. Finn nummeret du markert ned når du løst for området til en av de matchende ender og doble det til å stå for den andre enden.
2. 2
   Legg opp de områdene av sidene av prismene. Hvis prisme har trekantet ender, vil du være å legge opp tre sider, hvis de er femkantede, vil du bli utvidet med fem sider, osv. Hvis prismet er sylindrisk, trenger du ikke å legge til noe som det er bare en "side ".
3. 3
   Legg det totale området av endene til det totale arealet av sidene. Dette gir deg total areal av prisme.