Forventet verdi er et konsept ansatt i statistisk analyse. Det er et vektet gjennomsnitt tilnærming som innebærer å multiplisere hvert mulig utfall i en situasjon med sin sannsynlighet for å komme frem til det forventede resultatet. Forventet verdi fungerer som et gjennomsnitt, og kan ofte være en umulig utfallet i seg selv, for eksempel, er den forventede verdien av en seks-sided dø roll 3.5. For å beregne en forventet verdi, må du få en forståelse av hvert utfall i en situasjon og dens sannsynlighet.
Trinn
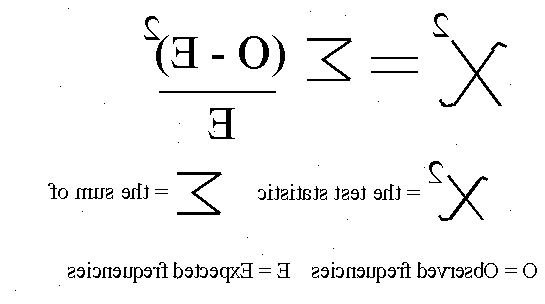
- 1Gjør deg kjent med situasjonen på hånden. Før opplisting av mulige utfall og sannsynligheter, sørg for å ha en helhetlig forståelse av situasjonen der et utfall blir generert. For eksempel vurdere en die-rullende spill som koster 10€ per spill. En seks-sided dø er rullet én gang og pengepremier avhengig av antall rullet. Rolling en 6 seire deg 25€; rulle en fem vinner du 15€; rulle et annet nummer resultatene på ingen utbetaling.
- 2Nummerere alle mulige utfall. Det hjelper å lage en liste over alle mulige utfall i den gitte situasjonen. I eksempelet ovenfor, er det seks mulige utfall. De er: (1) rulle en 1 og mister 10€ (2) rulle en to og mister 10€ (3) rulle en tre og mister 10€ (4) ruller en 4 og mister 10€ (5) rulle en 5 og vinne 10€ og (6) rulle en 6 og vinne 15€. Legg merke til at 10€ inngangsbilletten trekkes fra hvert utfall å komme frem til netto resultat.
- 3Bestem sannsynligheten for hvert utfall. I dette tilfellet, er sannsynligheten for at hver av de 6 utfall den samme. Når rulle en seks-sided dø, er sjansen for et bestemt tall blir rullet en i seks, eller 16,7 prosent. Det er nyttig å liste disse sannsynlighetene ved siden av sine resultater, spesielt i tilfeller mer komplisert enn en enkel terning kast.
- 4Beregne forventet verdi. Forventet verdi er beregnet med resultatene og deres sannsynligheter. Formelen er som følger: O1 * P1 + O2 * P2 + O3 * P3, etcetera. "O" termer representerer de ulike utfall, og "P" vilkår representerer sannsynligheten for disse resultatene.
- Fortsetter med eksempelet ovenfor, er den forventede verdi av terningspillet: (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (-10 * 0,167) + (10 * 0,167) + (20 * 0,167), eller - 5€ 0,67. Derfor, når du spiller terningspill, bør du forvente å miste 5€ 0,67 per kamp.
- 5Forstår konsekvensene av forventet verdi beregning. I eksempelet ovenfor, ble det fastslått at de forventede gevinster av spillet var - 5€ 0,67 per rull. Dette, selvfølgelig, er en umulig utfallet i seg selv, du kan bare enten taper 10€ seier 10€ eller vinne 15€. Imidlertid er den forventede verdi nyttig som en langsiktig snitt figur. Hvis du spiller dette terningspillet om og om igjen, vil du miste et sted nær 5€ 0,67 per kamp i gjennomsnitt. Derfor er dette spillet ikke er spesielt gunstig for spilleren.
- Jo flere ganger situasjonen er gjentatt, desto mer nøyaktig forventet verdi vil speile den faktiske gjennomsnittlige utfallet. For eksempel kan du spille spillet over fem ganger på rad, og taper hver gang, noe som resulterer i et gjennomsnittlig tap på 10€. Men hvis du skulle spille spillet 100 ganger eller enda mer, ville den gjennomsnittlige gevinsten begynne å reflektere den forventede verdien veldig pent. Dette prinsippet er avledet fra det treffende navnet "store talls lov."
- Det enkle spillet ovenfor illustrerer prinsippet som gambling opererer. Den gjennomsnittlige utbetalingen er negative, noe som betyr at huset vil tjene på spillet. Men tiltrekker lokke av en mulig stor utbetaling spillere til spillet.
Tips
- For situasjoner der det er mange utfall, kan du opprette en datamaskin regneark til å beregne forventet verdi fra resultatene og deres sannsynligheter.
- Beregningene ovenfor vil også arbeide når det uttrykkes i andre valutaer.
Ting du trenger
- Blyant
- Paper
- Kalkulator
