Wkono

Hvordan lære trigonometri

Trigonometri er den grenen av matematikken som omhandler studere trekanter. Det er veldig lett å forstå hvis nærmet i riktig måte. Denne artikkelen vil hjelpe deg å komme i gang å lære trigonometri.

Trinn

Hvordan lære trigonometri. Frisk opp dine grunnleggende matematiske ferdigheter.
Hvordan lære trigonometri. Frisk opp dine grunnleggende matematiske ferdigheter.
  1. 1
    Frisk opp dine grunnleggende matematiske ferdigheter. Disse omfatter kjennskap algebra og algebraical manipulering så vel som geometrien.
    • Øv algebraisk manipulasjon. Algebraisk manipulasjon er en svært grunnleggende ferdighet som er nødvendig for å studere noen gren av matematikken.
      1. Lær å endre emnet på noen ligningen.
      2. Lær å løse lineære og kvadratiske likninger.
      3. Lær å løse lineære likninger og lineære / kvadratisk par av likninger.
    • Lær grunnleggende geometri. Geometri er veldig nært knyttet til trigonometri og spiller en viktig rolle i å løse trigonometriske problemer.
      1. Lær egenskapene til en sirkel.
      2. Lær egenskapene til innvendige og utvendige vinkler av polygoner inkludert trekanter.
      3. Lær de tre ulike typer trekanter dvs. isosceles, likesidet og scalene.
    • 2
      Begynn med å studere rettvinklede trekanter. Rettvinklede trekanter er lett å studere og vil gi deg en god forståelse av grunnleggende trigonometri og de tre trigonometriske forholdstall.
      • Gjør deg kjent med de tre sider av en rettvinklet trekant.
        1. Hypotenusen er den siden som er motsatt av den rette vinkelen. Det er den største siden av noen rettvinklet trekant.
        2. De to andre sidene er kalt bena i trekanten. Hvis du velger hvilken som helst vinkel i trekanten (foruten den rette vinkelen), vil du se at det ene benet er ved siden av vinkelen, og det andre benet er motsatt tilstøtende> vinkelen.
      • Gjør deg kjent med de tre trigonometriske forholdstall, bunnen av trigonometri:
        1. Sinus av en hvilken som helst vinkel er forholdet mellom lengden av den siden som er motsatt den til lengden av hypotenusen.
        2. Cosinus av alle vinkler er forholdet mellom lengden av den side som grenser til den til lengden av hypotenusen.
        3. Tangens til hvilken som helst vinkel er forholdet mellom sinus til vinkelen til cosinus til vinkelen. Det er ofte også tatt som forholdet mellom den motsatte til det tilstøtende. Den første definisjonen er særlig til hjelp i å løse trigonometriske likninger og beviser identiteter mens andre er tilstrekkelig for en grunnleggende studie av trigonometri.
      • 3
        Gå videre til non-rettvinklede trekanter.. Fordi ikke-rette trekanter ikke har en rett vinkel (som er den form for definisjon), de tre trigonometriske forhold spille en mindre rolle her (selv om de også kan brukes i enkelte situasjoner.) Snarere to andre regler blitt svært viktig: Sinus regelen, og The cosinus regelen. Følgende artikler forklare disse reglene i detalj.

      • 4
        Lær å måle vinkler i radianer. Radianer er et alternativ til grader som en måte å måle vinkler. I 180 o, det er pi, eller ca 3,142, radianer. Radianer er spesielt nyttig når det gjelder å undersøke egenskapene til en sirkel, og brukes også i fysikk i studiet av bølger og enkel harmonisk bevegelse.
      • 5
        Lær de tre andre trigonometriske forholdstall. Det er tre mer trigonometriske forholdstall:
        1. Sekans. Det er det omvendte av den sinus dvs. 1/sin ofte kalles 'cosec' eller 'CSC'.
        2. Sekant. Det er den resiproke av cosinus ofte kalt «sek '.
        3. Cotangent. Det er det omvendte av den tangent ofte kalles 'vugge'.
      • 6
        Øv løse trigonometriske likninger. Trigonometriske likninger er (du gjettet det) ligninger involverer trigonometriske funksjoner. Trigonometriske likninger kan vanligvis løses ved manipulering av ligningen for å inneholde bare én trigonometriske forholdet. De følgende metoder ble anvendt for å konvertere en ligning som inneholder mer enn en trigonometrisk rasjon til en ligning som inneholder bare én:
        • Dele hele ligningen med en trigonometriske sikt. For eksempel, hvis en ligning har en løpetid på sinus, så vel som et begrep i cosinus, dele hele ligningen av cosinus. Begrepet i sinus blir et begrep i tan, og begrepet i cosinus blir en. Dermed har du en ligning som bare inneholder brunfarge.
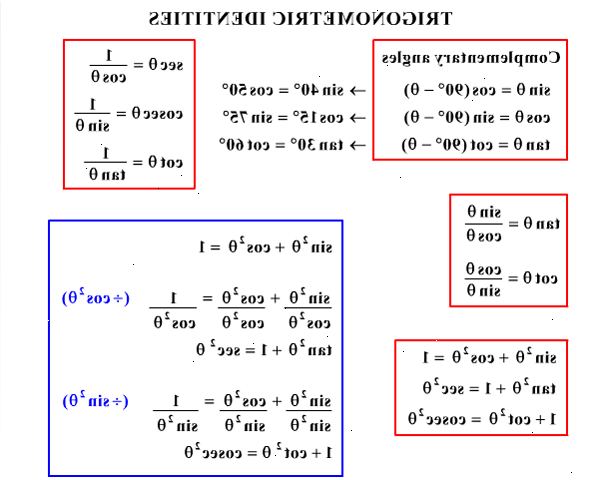
        • Ved hjelp av en trigonometrisk identitet. Trigonometriske identiteter er "ligninger" som alltid er sant. To trigonometriske identiteter er skrevet under:
          sin 2 x + cos 2 x = 1
          1 + tan 2 x = sek 2 x.
          Således hvis du hadde en ligning som inneholder ett semester i sinus 2 x og ett i cosx, ville du erstatte begrepet i sinus 2 x med 1 - cos 2 x fra første identitet ovenfor. Det ville resultere i en kvadratisk i cosx, som du bør vite hvordan du skal løse (sier det i første trinn).

Tips

  • Du trenger en vitenskapelig kalkulator.
  • Se på fasiten hvis du står fast.
  • Hvis du har problemer, spør en lærer eller en god student.
  • Gjennomgå algebra og geometri, spesielt hvis du er svak.
  • Kjøp en vinkelmåler.
  • Husk at matematikk er en måte å tenke på, ikke en haug med formler for å lære. Utvikle konsepter og skjerpe tenkning ferdigheter gjennom å løse problemer.