Enhetssirkelen er det beste verktøyet for å ha når du arbeider med trigonometri, hvis du virkelig kan forstå hva enhetssirkelen er og hva den gjør, vil du finne trig mye enklere.
Trinn
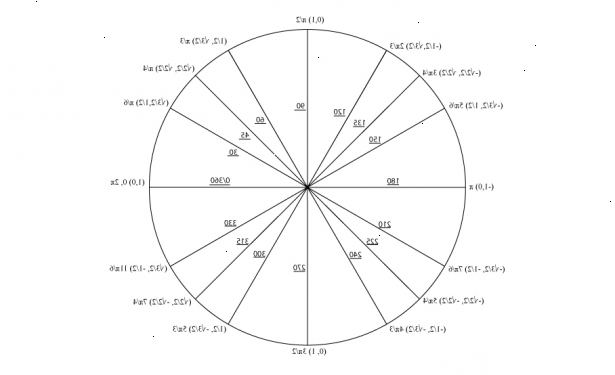
- 1Vet hva enhetssirkelen er. Enhetssirkelen er en sirkel, sentrert i origo, med en radius på 1. Recall fra kjeglesnitt at ligningen er x 2 + y 2 = 1. Denne sirkelen kan brukes til å finne visse "spesielle" trigonometriske forhold så vel som hjelpemiddel i grafisk fremstilling. Det er også et reelt tall linje pakket rundt sirkelen som fungerer som inngangsverdien ved vurdering av trigonometriske funksjoner.
- 2Vet de seks trigonometriske forholdstall. Vit at
- sinθ = motsatt / hypotenusen
- cosθ = tilstøtende / hypotenusen
- tanθ = motsatt / tilstøtende
- cscθ = 1/sin
- secθ = 1/cos
- cotθ = 1/tan.
- 3Forstå hva en radian er. En radian er en annen måte å måle en vinkel. En radianer er vinkelen nødvendig slik vedlagte buelengde er lik radien lengde. Merk at det ikke spiller noen rolle størrelse eller retning av sirkelen. Du trenger også å vite antall radianer i en full sirkel (360 grader). Husk at omkretsen av en sirkel er gitt ved 2πr så det er 2π radius tiltak i omkrets. Siden en radian per definisjon er vinkelen der radius lengde lik buelengden, det er 2π radianer i en full sirkel.
- 4Kunne konvertere mellom radianer og grader. Det er 2π radianer i en full sirkel, eller 360 grader. Så:
- 2πradian = 360 graders
- radian = (360/2π) grad
- radian = (180 / π) grad
- og
- grad = 2πradian
- grad = (2π/360) radian
- grad = (π/180)
- 5Kjenn "spesielle" vinkler. De spesielle vinkler i radianer er π / 6, π / 3, π / 4, π / 2, π, og multipler av alle (f.eks 5π / 6)
- 6Vet og huske trigonometriske identiteter som gir de seks trigonometriske funksjoner for alle vinkler. Å utlede disse, må du se på enhetssirkelen. Husk at det er et reelt tall tråd viklet rundt enhetssirkelen. Punktet på antall linje refererer til antall radianer i vinkelen dannet. For eksempel Punktet π / 2 på den virkelige antall linje korresponderer med det punkt på sirkelen med radius danner en vinkel på π / 2 med den positive horisontal radius. Kunsten å finne de trigonometriske verdier av alle vinkler, er derfor å finne koordinatene til det punktet. Hypotenusen er alltid en, som det er radien av den sirkel, og siden enhver tall dividert med en i seg selv, og den motsatte side er lik y-verdi, følger det at den sinus-verdi er y-koordinaten for det punktet. Cosinus verdien følger en lignende logikk. Cos lik den tilstøtende side dividert med hypotenusen, og igjen, som hypotenusen alltid er 1, og den tilstøtende side tilsvarer x-koordinaten, følger det at cosinus-verdien er x-koordinaten av det punktet. Tangenten er litt vanskeligere. Tangenten til en vinkel i en rettvinklet trekant er lik den motsatte side dividert med den tilstøtende side. Problemet er at det ikke er konstant i nevneren som i de foregående eksemplene, så du må være litt mer kreativ. Husk at den motsatte siden er lik y-koordinat og tilstøtende side er lik x-koordinat, så ved å erstatte, bør du finne at tangenten er lik y / x. Ved hjelp av dette kan du finne de inverse trigonometriske funksjonene ved å ta den gjensidige av disse formlene. For å oppsummere, her er de identiteter.
- sinθ = y
- cosθ = x
- tanθ = y / x
- CSC = 1 / y
- sek = 1 / x
- sprinkelseng = x / y
- 7Finn og huske de seks trigonometriske funksjoner for vinkler på aksene. For vinkler som er multipler av π / 2 som 0, π / 2, π, 3π / 2, 2π etc. Finne trigonometriske funksjoner er like enkelt som avbildet vinkelen på aksene. Hvis terminalen side er langs x-aksen, vil synden bli 0 og cos vil være enten 1 eller -1 avhengig av hvilken retning ray poeng. Tilsvarende, hvis terminalsiden er langs y-aksen, vil synd være enten 1 eller -1 og cos vil være 0.
- 8Finn og huske de seks trigonometriske funksjoner av spesiell vinkel π / 6. Start med å tegne vinkelen π / 6 på enhetssirkelen. Du vet hvordan du skal finne sidelengdene for spesielle rettvinklede trekanter (30-60-90 og 45-45-90) gitt den ene siden, og som π / 6 = 30 grader, er denne trekanten en av disse spesielle tilfellene. Så hvis du husker, er det korte ben 1/2 hypotenusen, slik at y-koordinaten er 1/2, og det lange ben er √ 3 ganger den kortere ben, eller (√ 3) / 2, slik at x-koordinaten er (√ 3) / 2. Koordinatene for dette punktet er ((√ 3) / 2,1 / 2) Nå bruker identiteter i forrige trinn for å finne at:
- sinπ / 6 = 1/2
- cosπ / 6 = (√ 3) / 2
- tanπ / 6 = 1 / (√ 3)
- cscπ / 6 = 2
- secπ / 6 = 2 / (√ 3)
- cotπ / 6 = √ 3
- 9Finn og huske 6 trigonometriske funksjoner av den spesielle vinkel π / 3) vinkelen π / 3 har et punkt på omkretsen hvor x-koordinaten er lik y-koordinaten i den π / 6 vinkel, og y-koordinaten er den samme som X-koordinat. Så, poenget er (1/2, √ 3/2). Derfor følger det at:
- sinπ / 3 = (√ 3) / 2
- cosπ / 3 = 1/2
- tanπ / 3 = √ 3
- cscπ / 3 = 2 / (√ 3)
- secπ / 3 = 2
- cotπ / 3 = 1 / (√ 3)
- 10Finn og huske de seks trigonometriske funksjoner av spesiell vinkel π / 4. Forholdstallene for et 45-45-90 trekant er en hypotenus √ 2 og ben av en slik på enhetssirkelen, dimensjonene er som følger: og de trigonometriske funksjoner er:
- sinπ / 4 = 1 / (√ 2)
- cosπ / 4 = 1 / (√ 2)
- tanπ / 4 = 1
- cscπ / 4 = √ 2
- secπ / 4 = √ 2
- cotπ / 4 = 1
- 11Vet hvilke referansen vinkel å bruke. På dette punktet du har allerede funnet de trigonometriske verdiene av de tre spesielle referanse vinkler, men alle disse er i kvadrant I. Hvis du trenger å finne en funksjon av en større eller mindre spesiell vinkel, først finne ut hvilken referanse vinkelen er i samme "familie" av vinkler. For eksempel består den π / 3 familien av 2π / 3, 4π / 3, og 5π / 3. En god generell regel for å finne den vinkel referanse er å redusere fraksjonen så mye som mulig da se nederst nummer. # * Hvis det er et tre, er det i π / 3 familie
- Hvis det er en 6, er det i den π / 6 familien
- Hvis det er en 2, er det i den π / 2 familie
- Hvis det står alene, som π eller 0, er det i π familien
- Hvis det er en 4, er det i den π / 4 familie
- 12Vet om verdien er positiv eller negativ. Alle vinkler i samme familie har de samme verdier som trig referansen vinkel, men 2 vil være positiv og to vil være negativ.
- Hvis vinkelen er i kvadrant I, alle trig verdiene er positive
- Hvis vinkelen er i kvadrant II, alle trigonometriske verdier er negative unntatt synd og CSC.
- Hvis vinkelen er i kvadrant III, alle trigonometriske verdier er negative bortsett tan og barneseng.
- Hvis vinkelen er i kvadrant IV, alle trig verdiene er negative med unntak av COS og sek.
