En trig ligningen er en ligning som inneholder ett eller flere trigonometriske funksjoner av variable trig arc x. Løse for x betyr å finne verdiene av trig buer som trig funksjoner gjør trig ligningen sant.
- Svar, eller verdier av løsningen buer, er uttrykt i grader eller radianer. Eksempler:
x = Pi / 3, x = 5Pi / 6, x = 3Pi / 2, x = 45 grader.; X = 37.12 grader.; X = 178,37 grader.
- Merk: På trig enhetssirkelen, de trigonometriske funksjoner av noen arc er de samme trigonometriske funksjoner av tilsvarende vinkel. De trigonometriske enhetssirkelen definerer alle trigonometriske funksjoner av variable arc x. Det er også brukt som bevis i å løse grunnleggende trigonometriske likninger og ulikheter.
- Eksempler på trigonometriske likninger:
- sin x + sin 2x = 1/2; tan x + barneseng x = 1,732;
- cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.
- De trigonometriske enheten sirkelen.
- Det er en sirkel med radius = 1 enhet, har O som opprinnelse. De trigonometriske enhetssirkelen definerer fire viktigste trigonometriske funksjoner av variable arc x som roterer mot klokka på den.
- Når buen, med verdi x, varierer på trig enhetssirkelen:
- Den horisontale aksen OAX definerer trigonometrisk funksjon f (x) = cos x.
- Den vertikale aksen definerer Øby den trigonometrisk funksjon f (x) = sin x.
- Den vertikale aksen AT definerer trigonometrisk funksjon f (x) = tan x.
- Den horisontale aksen BU definerer trigonometrisk funksjon f (x) = barneseng x.
- De trigonometriske enheten sirkelen brukes også til å løse grunnleggende trigonometriske likninger og grunnleggende trigonometriske ulikheter ved å vurdere de ulike posisjonene til arc x på denne sirkelen.
Trinn
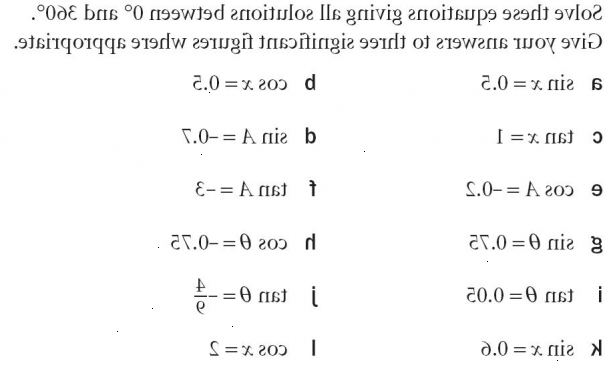
- 1Kjenn løse konseptet.
- For å løse en Trig ligning, forvandle det til en eller mange grunnleggende trigonometriske likninger. Løse trigonometriske likninger resulterer til slutt i å løse fire typer grunnleggende trigonometriske likninger.
- 2Vet hvordan å løse grunnleggende trigonometriske likninger.
- Det finnes fire typer av grunnleggende trigonometriske likninger:
- sin x = a, cos x = a
- tan x = a; barneseng x = a
- Løse vanlige trigonometriske likninger inntektene ved å studere de ulike posisjonene til buen x som roterer på trig sirkel, og ved hjelp av trigonometriske konverteringstabell (eller kalkulator). For å fullt ut vet hvordan å løse disse grunnleggende trigonometriske likninger, og lignende, se bok med tittelen: "trigonometri: Løse trigonometriske likninger og ulikheter" (Amazon E-bok 2010).
- Eksempel 1. Løs sin x = 0,866. To svar gitt av konverteringstabeller (eller kalkulator), og trig enhet sirkel:
- x1 = Pi / 3 + 2k.Pi
- x2 = 2n / 3 + 2k Pi
- Eksempel 2. Løs: cos x = -1 / 2
- x1 = 2n / 3 + 2k.Pi
- x2 =-2n / 3 + 2k.Pi
- Eksempel 3. Løs: tan (x - Pi / 4) = 0
- Svar: x = Pi / 4 + k.Pi
- Eksempel 4.. Løs barneseng 2x = 1,732
- Svar: x = Pi/12 + k.Pi / 2
- Det finnes fire typer av grunnleggende trigonometriske likninger:
- 3Lær transformasjoner som brukes til å løse trigonometriske likninger.
- Å forvandle en gitt trig ligning i grunnleggende trigonometriske seg, bruke vanlige algebraiske transformasjoner (factoring, felles faktor, polynom identiteter...), definisjoner og egenskaper av trigonometriske funksjoner, og trigonometriske identiteter. Det er om lag 31, blant dem de siste 14 trigonometriske identiteter, 19-31, kalles Transformation identiteter, siden de brukes i omformingen av trigonometriske likninger. Denne boken viser hvordan du kan forvandle en gitt trig ligning i grunnleggende trigonometriske likninger.
- 4Eksempel: trig likningen: sin x + sin 2x + sin 3x = 0 kan transformeres ved hjelp av trigonometriske identiteter, i et produkt av grunnleggende trigonometriske likninger:. 4cos x.sin (3x / 2) cos (x / 2) = 0. De enkle trigonometriske likninger som skal løses er: cos x = 0; sin (3x / 2) = 0, og cos (x / 2) = 0.
- 5Finn de buer som trig funksjoner er kjent.
- Før lære å løse trigonometriske likninger, må du vite hvordan du raskt finne de buer som trig funksjoner er kjent. Konvertering verdier av buer (eller vinkler) er gitt av trigonometriske tabeller eller kalkulatorer.
- Eksempel: Etter å løse, får cos x = 0,732. Kalkulatorer gi løsningen arc x = 42.95 grader. De trigonometriske enhetssirkelen vil gi andre løsning buer som har samme cos verdi.
- 6Graf løsningen buer på trig enhetssirkelen.
- Du kan tegne grafen for å illustrere løsningen buer på trig enhetssirkelen. Termineringspunktene av disse løsning buer utgjør regulære polygoner på trig sirkel. For eksempler:
- Termineringspunktene av løsningen buer x = Pi / 3 + k.Pi / 2 utgjør en firkant på trig enhetssirkelen.
- Løsningen buer x = Pi / 4 + k.Pi / 3 er representert ved toppunktene til et likesidet sekskant på trig enhetssirkelen.
- 7Lær metoder for å løse trigonometriske likninger.
- Dersom den gitte trig ligning inneholder bare én trigonometrisk funksjon, løse den som en enkel trigonometrisk ligning. Dersom den gitte ligning inneholder to eller flere trigonometriske funksjonene er det 2 tilnærminger i løse, avhengig transformasjon mulighet.
- A. Approach en.
- Dersom den gitte trig ligning inneholder bare én trigonometrisk funksjon, løse den som en enkel trigonometrisk ligning. Dersom den gitte ligning inneholder to eller flere trigonometriske funksjonene er det 2 tilnærminger i løse, avhengig transformasjon mulighet.
- 8Transformer den oppgitte trigonometrisk ligning i et produkt i form:... F (x) g (x) = 0, eller f (x) g (x) t (x) = 0, hvor f (x), g ( x) og h (x) er grunnleggende trigonometriske likninger.
- Eksempel 5. Løs: cos x + cos 2x + cos 3x = 0.
- Løsning: Gjør det til et produkt, ved hjelp av trigonometriske identiteter:
- cos 2x (2cos x + 1) = 0. Deretter løse to grunnleggende trigonometriske likninger:
- cos 2x = 0 og 2cos x + 1 = 0
- Eksempel 6. Løs: sin x - sin 3x = cos 2x.
- Løsning: forvandle det til et produkt, ved hjelp av trigonometriske identiteter:
- -Cos 2x (2sin x + 1) = 0. Deretter løse de to grunnleggende trigonometriske likninger:
- cos 2x = 0 og 2sin x + 1 = 0.
- B. Approach to.
- Transformere den gitte trig ligningen til en Trig ligningen har bare én unik trigonometrisk funksjon som variabel. Det er et par tips om hvordan du velger riktig variabel. Den vanlige variabler å velge er: sin x = t, cos x = t, cos 2x = t, tan x = t og tan (x / 2) = t.
- Eksempel 7. Løs: sin ^ 2 x + sin ^ 4 x = cos ^ 2 x.
- Løsning. Ring cos x = t og transformere den gitte ligningen i en ligning har bare t som variabel: t ^ 4 - 4t ^ 2 + 2 = 0. Løs denne likningen for t og deretter løse de grunnleggende trigonometriske ligningen cos x = t for å få x.
- Eksempel 8. Løs: tan x + 2 tan ^ 2 x = barneseng x + 2.
- Løsning. Ring tan x = t. Transformere den gitte ligningen i en ligning med t som variabel: (2t + 1) (t ^ 2 - 1) = 0. Løse for t fra dette produktet, og deretter løse de grunnleggende trigonometriske likningen tan x = t for x.
- 9Løs spesielle typer trigonometriske likninger.
- Det er noen spesielle typer trigonometriske likninger som krever noen spesifikke transformasjoner.
- 10Lær den periodiske eiendom trigonometriske funksjoner.
- Alle trigonometriske funksjoner er periodisk betyr at de kommer tilbake til samme verdi etter en rotasjon for en periode. Eksempler:
- Funksjonen f (x) = sin x har 2Pi som perioden.
- Funksjonen f (x) = tan x har Pi som perioden.
- Funksjonen f (x) = sin 2x har Pi som perioden.
- Funksjonen f (x) = cos (x / 2) har 4Pi som perioden.
- Dersom perioden er angitt i problemet / test, må du bare finne løsningen arc (er) x innenfor denne perioden.
- MERK: Etter å løse, kan du sjekke svarene ved hjelp av en grafisk kalkulator til direkte grafen den gitte trig ligningen R (x) = 0. Svarene (reelle røtter) vil bli gitt i desimaler. For eksempel er Pi gitt ved verdien 3,14
- Alle trigonometriske funksjoner er periodisk betyr at de kommer tilbake til samme verdi etter en rotasjon for en periode. Eksempler:
