Finne domenet til en funksjon er noe du kan bli bedt om å gjøre i matte klasse, spesielt i algebra og utover. Domenet er ansett som en av de viktigste bitene av informasjon om en funksjon. Disse trinnene vil lære deg hvordan å finne domenet til en funksjon.
Trinn
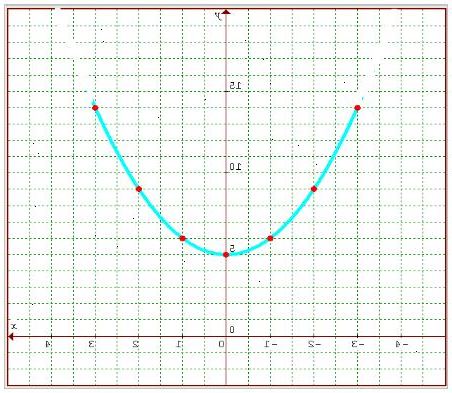
- 1Lær definisjonen av domenet. Før du kan begynne å finne domenene til spesifikke funksjoner, må du først ha en sterk forståelse av hva domenet er. Domenet er definert som det sett med inngangsverdier for hvilken den funksjon frembringer et utgangssignal verdi. Med andre ord, er domenet komplett sett med x-verdier som kan plugges inn i en funksjon for å produsere en y-verdi.
- 2Identifisere den typen funksjon som du arbeider med. Strategiene for å finne domenet til en funksjon avhengig av egenskapene til funksjonen. Når du først begynner å lære om funksjonene, kan du bli gitt eksempel problemer som bare liste et sett av punkter (dvs. x-verdier og tilhørende y-verdier). For disse typer av funksjoner, er domene bare listen med x-verdier for hvert av punktene. For en polynomisk funksjon uten radikaler eller variabler i nevneren, er domenet alle reelle tall. Utover disse enkle funksjoner, er det to spesielle tilfeller som du må se opp for:
- Fraksjoner med en variabel i nevneren
- Kvadratrøtter
- 3For fraksjoner, sette nevneren lik null. Når finne domenet til en brøk funksjon, må du utelukke alle x-verdier som gjør nevneren lik null, fordi du aldri kan dele på null. Så, skrive nevneren som en ligning og sette den lik 0.
- Løs likningen. Bruk algebraiske metoder, løse ligningen for de verdier som gjør nevneren lik 0. Det kan bli nødvendig å faktor eller bruke andre metoder. For kvadratiske og andre høyere orden polynomer, vil du ha flere svar.
- Legg merke til at telleren er helt irrelevant i denne prosessen. Telleren kan være en konstant eller et polynom, det vil ikke endre domenet til funksjonen.
- Eksempel
- Løs likningen. Bruk algebraiske metoder, løse ligningen for de verdier som gjør nevneren lik 0. Det kan bli nødvendig å faktor eller bruke andre metoder. For kvadratiske og andre høyere orden polynomer, vil du ha flere svar.
- 4
- 5For kvadratrøtter, skrive roten som en ulikhet. Med kvadratrøtter, må radicand (uttrykket under radikale sign) alltid være 0 eller større. Så, skrive en ulikhet som setter radicand å være større enn eller lik 0..
- Løs ulikheten. Ved hjelp av algebraiske metoder, slik som factoring, løse ulikheten for alle x-verdier som gjør radicand større enn eller lik 0..
- Husk at for ulikheter med flere løsninger, må du lage en rekke tråd med nuller angitt, og deretter teste hver intervall for å avgjøre om det gjør uttrykket positiv eller negativ. Med det formål å finne domenet, velger bare de intervaller som er positive.
- Merk at dette gjelder ikke bare for å kvadratrøtter, men til alle partalls-røtter. Det betyr imidlertid ikke gjelde for oddetall røtter, fordi det er helt greit å ha negativer etter ulike røtter.
- Eksempel
- Løs ulikheten. Ved hjelp av algebraiske metoder, slik som factoring, løse ulikheten for alle x-verdier som gjør radicand større enn eller lik 0..
- 6
- 7Korrekt skrive domenet. Riktig notasjon for domenet er lett å lære, men det er viktig at du skriver det riktig å uttrykke det riktige svaret og få full poeng på oppgaver og tester. Her er noen ting du trenger å vite om å skrive domenet til en funksjon.
- Formatet for å uttrykke domenet er en åpen brakett / parentes, etterfulgt av de to endepunktene på domenet atskilt med et komma, etterfulgt av en lukket brakett / parentes.
- For eksempel, [-1,5). Dette betyr at domenet går -1-5.
- Bruk "[" og "]" for å indikere at en del er inkludert i domenet.
- Så i eksempel [-1,5), omfatter domene -1.
- Bruk "(" and ")" for å indikere at nummeret ikke er inkludert i domenet.
- Så i eksempel [-1,5), er 5 ikke i domenet. Domenet stopper vilkårlig kort av fem, dvs. 4.999...
- Bruk "U" (som betyr "union") for å koble deler av domenet som er atskilt med et mellomrom.
- For eksempel, [-1,5) U (5,10]. Dette betyr at domenet går -1 til 10, inklusive, men at det er et gap i domenet ved 5. Dette kan være et resultat av, for eksempel en funksjon med "x - 5" i nevneren.
- Du kan bruke så mange "U" symboler som nødvendig hvis domenet har flere hull i den.
- Bruk uendelig og negative uendelig tegn til å uttrykke at domenet går på uendelig i begge retninger.
- Bruk alltid (), ikke [], med uendelig symboler.
- Eksempler
- Formatet for å uttrykke domenet er en åpen brakett / parentes, etterfulgt av de to endepunktene på domenet atskilt med et komma, etterfulgt av en lukket brakett / parentes.
- 8
- Å uttrykke at domenet til funksjonen er alle reelle tall, skriver det slik:
- 9
- 10Praksis. Ved hjelp av disse trinnene, kan du finne domenet til en funksjon. Imidlertid kan håndtere radikaler og nevnerne i kombinasjon være forvirrende og vanskelig. Så, praksis med eksempler som er mer komplekse enn de som vises her å virkelig mestre begrepet finne domenet.
