Wkono

Hvordan bevise Pythagoras 'læresetning

Den Pythagoras 'læresetning lar deg regne ut lengden av den tredje siden i en rettvinklet trekant når de andre to er kjent. Og mer.
Den er oppkalt etter Pytagoras av Samos, som oppdaget og beviste det. Han levde rundt 550 f.Kr. i Hellas. Det er ingen grunn til å tro at teoremet til å være sant, kan du bevise det, så du vet det er.

Trinn

Hvordan bevise Pythagoras 'læresetning. Anta at vi har fire kongruente (grå) rettvinklede trekanter.
Hvordan bevise Pythagoras 'læresetning. Anta at vi har fire kongruente (grå) rettvinklede trekanter.
  1. 1
    Anta at vi har fire kongruente (grå) rettvinklede trekanter. Sier de har beina på lengde a, b og hypotenusen lengde ca.
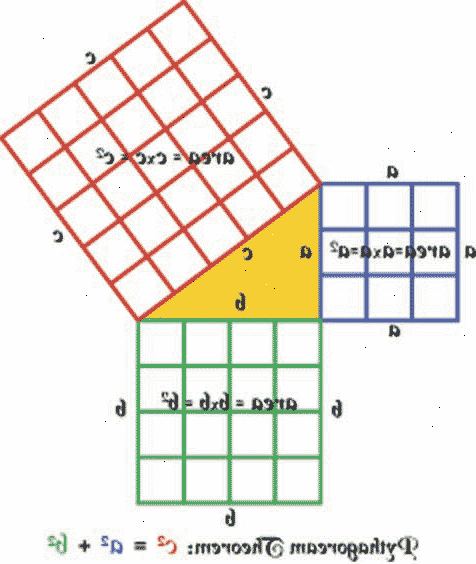
    Pythagoras 'læresetning sier at summen av kvadratene av de to bena i en rettvinklet trekant er lik kvadratet av hypotenusen. Så i utgangspunktet vi trenger å bevise
    a 2 + b 2 = c 2
  2. 2
    Ordne dem i en firkant med sider (a + b) av (a + b), som dette.
    • Den grønne form utelatt av trekantene ser litt ut som en firkant. Men er det virkelig et kvadrat?
    • Den har fire like sider, er lengden alltid c.
    • Du kan rotere (slå) hele ordningen med 90 grader, og det vil være nøyaktig den samme. Du kan gjenta dette så mange ganger du vil. Dette er bare mulig dersom de fire vinkler i hjørnene er like.
    • Hvis du har fire like sider og fire like vinkler du må ha et kvadrat.
  3. 3
    Nå settes de samme fire trekanter i den samme plassen, men nå gjør det annerledes, som dette.
    • Den blå firkanten har sider av lengde b, har den røde sider av lengde en.
  4. 4
    Nå sammenligne de to arrangementene.
    • Det samlede areal av de to arrangementer var den samme. I begge tilfeller har vi brukt en firkant av (a + b) av (a + b).
    • I begge ordninger delvis vi dekket overflaten med nøyaktig samme beløp, fire grå trekanter som ikke overlapper hverandre.
    • Dette betyr at også i området utelatt av trekantene må være lik i begge disse konstruksjonene.
    • Dette innebærer at arealet av det blå og det røde firkantet tilsammen må være lik arealet av den grønne firkanten.
  5. 5
    Det blå området er en 2, det røde området 2 b og grønt område c 2.
  6. 6
    Kort sagt: en 2 + b 2 = c 2. Derav Pythagoras 'læresetning er bevist!

Tips

  • Pythagoras 'teorem gjelder for rettvinklede trekanter bare.
  • Du kan finne andre matematiske bevis på. Ikke alle high school ting er der, men de jobber med det.
  • Det er uendelig mange Pythagoras trillinger, der alle sidene i trekanten er hele tall. Men (3, 4, 5) og (5, 12, 13) er favoritt blant matematikk lærere.
  • Det er OK å tenke den andre veien rundt. Hvis pythagorean teorien gjelder en trekant, si deres lengder er 3, 4, og 5, må det være en rett vinkel eller annet sted i den trekant!
  • Det er minst 367 forskjellige måter av teoremet. Dette er en av de enkleste.