Hvordan beregne kubikkroten for hånd

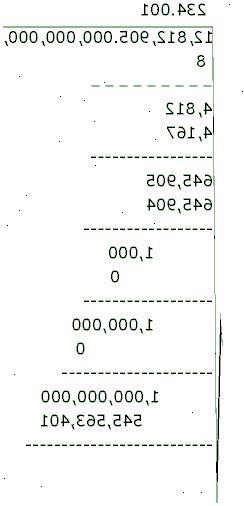
Beregning kubikkroten for hånd

1. 1
   Skriv ned antall som du vil beregne kubikkroten, skille sifrene i grupper på tre, som starter på desimaltegn fra begge retninger. Tegne en kube radikal skilt over nummeret, og sette et punktum over radikale rett over desimaltegnet i antall. For eksempel, la oss beregne kubikkroten av 10, så vi skille det som 10. 000 000 kroner.
2. 2
   Begynn med den lengst til venstre gruppe av tall (er), og finne den største heltall hvis kuben er mindre enn eller lik den. Skriv heltallet ovenfor radikal, og dens kuben under det første gruppen. Tegne en linje under som kube, og trekke det fra den første gruppen. I vårt eksempel 2 ^ 3 = 8 <10 <3 ^ 3 = 27, så skriv to over radikale, skrive åtte under første gruppen, og trekke det fra den første gruppen, noe som resulterer i to.
3. 3
   Bringe ned den neste gruppen av numre til resten, og trekke en vertikal linje til venstre for det resulterende tall. Til venstre for den vertikale linje, skrive tre hundre ganger kvadratet av antall over radikal, et plusstegn, tretti ganger så mange over den radikale, en multiplikasjon tegn, en understreket bokstav, en annen plusstegn, en annen understreket bokstav, eksponenten 2, tilsvarer en skilt, og noen mellomrom for svaret. For vårt eksempel, få ned tre 0-tallet. 300 ganger kvadratet av to er 1200, er 30 ganger 2 60, så skriv "1200 60 * _ + _ ^ 2 = (mellomrom)" til venstre for den vertikale linjen.
4. 4
   Finn de største heltall N som ville passe inn i begge understrek steder, og gi et tall i det tomme rommet slik at heltall N ganger tallet er mindre enn dagens resten. Sett heltall N over den radikale og inn både understrek steder, beregnes antallet til høyre for likhetstegnet, multiplisere dette tallet med N, skriver produktet under dagens resten, tegne en linje under det, og trekke fra for å få den nye resten. For vårt eksempel, er heltall 1, 1200 60 * 1 1 ^ 2 = 1261, og 1 * 1261 = 1261, som trekkes fra 2000 er 739. Dersom det aktuelle svaret ovenfor radikalet har den ønskede nøyaktighet, stopp. Ellers går du videre til neste trinn.
5. 5
   Gjenta de to foregående trinn for å finne det neste sifferet i kubikkroten.
6. 6
   Resultatet ovenfor den radikale er kubikkroten, nøyaktig tre siffer. I vårt eksempel er kubikkroten av 10 2.15. Kontroller at ved å beregne 2,15 ^ 3 = 9.94, som tilnærmet 10. Hvis du trenger større nøyaktighet, er det bare å fortsette prosessen.