Hvordan beregne geometrisk gjennomsnitt

Geometrisk gjennomsnitt er et matematisk begrep som er relatert til, men lett forveksles med den mer brukte aritmetisk gjennomsnitt. For å beregne det geometriske gjennomsnittet, bruker du en av metodene nedenfor.

Trinn

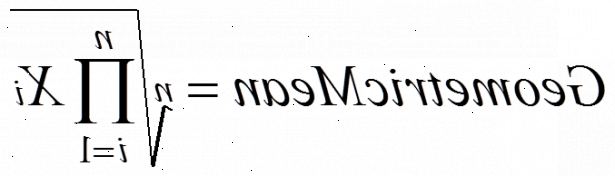
Hvordan beregne geometrisk gjennomsnitt. Finn tallene du ønsker å gjennomsnittet.

To tall: enkel metode

1
Finn tallene du ønsker å gjennomsnittet.
- Ex. 2 og 32.
2
Multiplisere dem sammen.
- Ex. 2 x 32 = 64.
3
Beregn kvadratroten av nevnte nummer.
- Ex. √ 64 = 8.

To tall: detaljert metode

1
Plugg dine tall i ligningen nedenfor.
Hvis tallene er 10 og 15, for eksempel, plugg i 10 for "first #" og 15 for "andre #."
2
Løs for X.
Start ved kryss-formere seg, noe som betyr multiplisere nummerpar diagonal til hverandre, og deretter å sette resultatene på motsatte sider av en = fortegn. Siden X * X er X ^ 2, bør ligningen se slik ut: X ^ 2 = (produkt av dine andre tall).
Å løse for X, finne kvadratroten av produktet. Hvis du er heldig, vil resultatene være ett nummer. Hvis ikke, kan du gi en desimal svar eller la svaret i kvadratroten form, avhengig av hva din instruktør foretrekker. Eksemplet nedenfor er i forenklet kvadratroten skjemaet.

Tre eller flere tall: enkel metode

1
Plugg dine tall i ligningen nedenfor.
Mean = (a ₁ × en _to... en _n) ^{1 / n}
- en ₁ er ditt første tallet, er en ₂ din andre nummer, og så videre
- n er antall oppføringer
2
Multiplisere tallene (a _1, a _2, etc.) Sammen.
3
Beregn n th roten av dette nummeret. Dette er den geometriske middelverdien.

Tre eller flere tall: detaljert metode

1
Finn loggen for hvert nummer og legge til logaritmiske verdier sammen.
Finn LOG knappen på kalkulatoren. Når du er klar, skriver du: (første rekke) LOG + (andre rekke) LOG + (tredje nummer) LOG [+ log av flere numre som nødvendig] =. Ikke unnlate å skrive = Eller nummeret du ser vil være loggen for siste nummer, ikke totalen.
- Ex. log 7 + log 9 + log 12 = 2,878521796...
2
Dividere summen av de logaritmiske verdier av det antall verdier dere lagt. Hvis du har lagt loggene av tre tall, dividere med tre.
- Ex. 2,878521796 / 3 = 0,959507265...
3
Finn antilog på resultatet. På kalkulatoren, trykker du på 2. funksjon (vanligvis gul) og deretter LOG andre> for å aktivere det sekundære funksjon av log-knappen, eller antilog. Dette resulterer verdi er det geometriske gjennomsnittet.
- Ex. antilog 0,959507265 = 9,109766916. Derfor er det geometriske gjennomsnittet av 7, 9, og 12. 9.12.

Tips

Forskjellen mellom aritmetisk og geometrisk gjennomsnitt:
- Hvis du ønsket det aritmetiske gjennomsnitt av tre, fire og 18, for eksempel, ville du legge 3 + 4 + 18, deretter dele på 3 fordi det er tre tall. Resultatet ville være 25/3 eller omtrent 8,333..., som viser at hvis du hadde tre verdier på 8,3333..., vil det gi den samme totale som de individuelle verdier av 3, 4 og 18. Det aritmetiske gjennomsnittet svar på spørsmålet: "Hvis alle de mengdene hadde samme verdi, hva ville denne verdien må være for å legge opp til samme total?"
- Derimot, de geometriske gjennomsnitt svarer på spørsmålet: "Hvis alle de mengdene hadde samme verdi, hva ville denne verdien må være for å ha samme produkt når multiplisert?" Så for å finne det geometriske gjennomsnittet av 3, 4 og 18, ville vi multipliserer 3 x 4 x 18. Dette vil gi oss 216. Vi vil deretter ta kubikk root (kubikk rot fordi det var tre originale tall). Svaret vil være seks. Med andre ord, siden 6 x 6 x 6 = 3 x 4 x 18, 6 er det geometriske gjennomsnittet av 3, 4 og 18..
Geometrisk gjennomsnitt på noe sett med tall alltid er mindre enn eller lik det aritmetiske gjennomsnitt av settet. Se wikipedia: AM-GM_inequality
Det geometriske gjennomsnittet gjelder kun for ikke-negative tall. I ord problemer der en geometrisk gjennomsnitt er hensiktsmessig, vil situasjonen normalt ikke fornuftig med negative tall.