Vi har alle hatt å stri med problemer i algebra kalles "ord problemer." En typisk ord problem innebærer å blande oppløsninger av gitte sterke til å få en viss mengde av blandingen ved en ønsket styrke. I denne artikkelen vil du lære en generell teknikk for å løse slike problemer.
Trinn
- 1For å forklare trinnene, vil vi bruke et bestemt utvalg problem:
- 2Hypatia har 20% og 15% løsninger av saltvann (salt) oppløsningen. Hvor mye av hver skal hun blande sammen for å få fem liter 18% saltløsning?
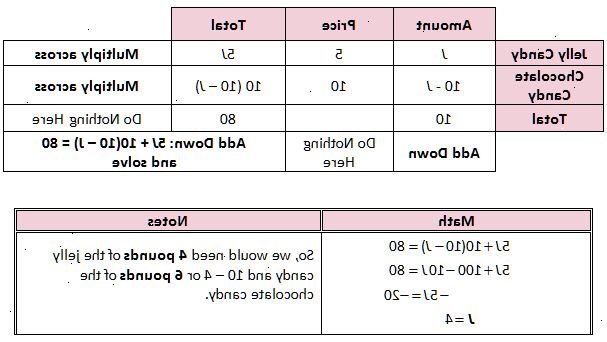
- 3Organisere informasjonen. Vanligvis har du tre prosenter, to ukjente mengder, og en kjent mengde. Den vanlige overordnede strukturen er:
- 4Bestem hvilken informasjon representerer den endelige styrke og mengde. I vårt eksempel er det endelige produktet skal være fem liter 18% salt løsning.
- 5Bytt ut informasjon om den endelige styrke og mengde.
- 6Erstatte de to andre prosenter. Det spiller ingen rolle hvilken du setter for A og som for B.
- 7Velg en variabel for en av de ukjente mengder. Det spiller ingen rolle hvilken du velger. For dette problemet, velger vi x for å representere mengden av 20%-ig oppløsning.
- 8Uttrykk mengden av den andre løsning som skal anvendes. Siden vi vet at beløpene må legge opp til 5 liter, og vi har allerede valgt x for 20% løsning, er mengden av den andre løsningen 5 - x.
- 9Fullfør multiplikasjon som er etter likhetstegnet.
- 10Fordel multiplikasjon over kvantitet 5 - x.
- 11Løs resten av ligningen.
- 12Tolke svaret. Vi valgte 20% for å gå med x, slik at x = 3 betyr at vi trenger 3 liter 20%-løsning. Det endelige beløpet skulle være 5 liter. Så som etterlater to liter for den andre, som var den 15%-løsning.
- 13Skriv ut din endelige svaret. I dette tilfellet ville vi skrive: Hypatia vil trenge 3 liter 20%-løsning og 2 liter 15% oppløsning for å få 5 liter en 18% løsning.
Ting du trenger
- Evnen til å løse et enkelt algebra ligning (f.eks * 0,20 x + 0,15 * (1-x) = 0,18)
