Wkono

Slik finne arealet av regulære polygoner

En vanlig polygon er en to-dimensjonal konveks figur som består av kongruente sider og vinkler like i mål. En konveks Figuren er en figur med vinkler mindre enn eller lik 180 grader.

Denne artikkelen omhandler hvordan man skal finne arealet av regulære polygoner med mer enn fire sider. Hvis du ønsker å vite arealet av en firkant, gå. Hvis du vil vite hvordan du skal finne arealet av en trekant, kan du gå

Trinn

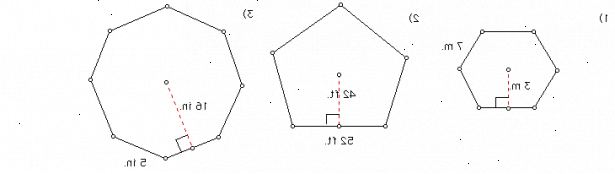
Slik finne arealet av regulære polygoner. Arealet av en hvilken som helst regelmessig mangekant, er gitt ved formelen.
Slik finne arealet av regulære polygoner. Arealet av en hvilken som helst regelmessig mangekant, er gitt ved formelen.
  1. 1
    Arealet av en hvilken som helst regelmessig mangekant, er gitt ved formelen:
    Område = (AXP) / 2,
    hvor a er lengden av den apothem og p en> er polygonets omkrets.
    Apothem er linjesegmentet fra midten av et regulært polygon til midtpunktet på en side. Perimeter kan finnes ved å multiplisere sidelengde med antall sider i mangekanten.
  2. 2
    Sammen med sidelengde, hvis lengden av apothem er også direkte til stede, vil det finne arealet av en slik polygon er ikke mer enn en kake tur. Bare plugg i verdiene av a og p a> i formelen og få området.
    For eksempel vurdere å finne arealet av en likesidet sekskant (6 sider) av sidelengde 10 enheter og apothem måling 5sqrt (3) enheter.
  3. 3
    Sammen med sidelengde, hvis lengden av apothem ikke er direkte gitt så den kan beregnes ved hjelp av følgende formel:
    a = (e / 2) x cot (180 0 / n),
    hvor a er lengden av den apothem, er s en> den sidelengde, og n er antallet av sider i mangekanten.
    • Som et eksempel, vurdere å finne arealet av en vanlig nonagon (9 sider) av sidelengde 5 enheter.
    • Finn apothem
    • Finn omkretsen
    • Finne arealet ved hjelp av formelen nevnt i trinn 1 ovenfor.

Tips

Advarsler

  • Hvis tegningen av oktogonen din (eller hva) har blitt delt opp i trekanter, og en trekant område er merket, så du trenger ikke å gjøre hele apothem virksomhet. Bare ta arealet av at en trekant, og multiplisere med antall sider i den opprinnelige polygonet.