En "heltall" er bare en fancy måte å si "et tall (ikke en delvis antall lignende, 1/2 eller 2.7), som kan være positive, negative eller null." (Eksempler på heltall er: 3, -12, 17, 0, 7000, -582, etc. Eksempler på ikke-heltall er:. 4/5, 3,08, -4,2, og -16 / 3) addisjon og subtraksjon kan regler får komplisert når du prøver å skrive dem ut. Bare husk at hver tillegg eller subtraksjon av to tall, enten de er begge positive, både negativt, eller en av hver, koker ned til de samme to spørsmål: 1) Har verdien "hoper seg opp" eller "avbryt ned?" og 2) er resultatet negativt eller positivt?
Trinn
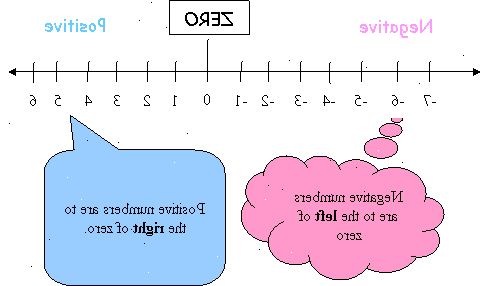
Del én: "hopet seg opp" vs "avbryter down"
- 1Forstå sentrale begreper. Hva menes med "hopet seg opp" og "avbryter down"? Vel, visualisere positive tall som svarte poker chips og negative tall som røde poker chips. Deretter akseptere det faktum at en svart utligner ett rødt.
- 4 + 7 er å sette en haug av fire svarte brikker på toppen av en haug av syv svarte brikker. Sluttresultatet: 11 svarte brikker. Derfor, 4 + 7 hauger opp til 11 år.
- -4 + (-7) Er å sette en haug av fire røde chips med en haug av syv røde chips. Resultat: 11 røde chips.
Derfor, -4 + -7 hauger opp til -11. - 4 + (-7) setter fire svarte brikker med 7 røde chips. De fire svarte utjevne 4 av 7 red. Resultat: 3 røde chips igjen. Derfor avbryter 4 + -7 til -3.
- -4 + 7 setter fire red med syv svart. De fire røde avbryte ut fire av de syv svarte. Resultat: 3 svarte brikker igjen. Derfor -4 + 7 kansellerer til tre.
- 2Hoper seg opp eller avbryte ned poker chips, avhengig av saken. Hver kombinasjon av 4, 7, -4, -7 og, om subtraksjon eller tillegg, oversettes direkte tilbake inn i en av fire muligheter som er beskrevet ovenfor. Men du må bruke den aktuelle strategien til hvert problem.
Del to: beregning trippel negativer
- 1Se etter det som kan kalles "triple negativer", slik som: ". -4 Til 7"
- 2Endre subtraksjon til å legge det motsatte. I dette tilfellet er den subtraksjon av de -7 endres til et "pluss pluss", som betyr at den opprinnelige -4 -. (-7) Er nå -4 + (7) Legg merke til at de 4 forblir negativ. En flott måte å huske dette er KCC, eller holde endring endring. Hold -4, endre - til +, så -7 til 7. Deretter legger og du vil ha et svar.
- 3Utjevne verdier. Fjern en svart brikke for hver rød chip før du går tom for en bestemt farge.
- 4Bestem på skiltet i svaret. Hvis haug av svarte brikker er større, er svaret positivt. Hvis haug av røde chips er større, er svaret negativt.
- Eksempel: -4 - (-7) blir da -4 + (7), som er det samme som (-4) + 7, som er lik tre.
- Eksempel: -12 - (-2) blir -12 + 2, som er -12 + 2, som er lik -10.
Del tre: beregning doble negativer
- 1Se etter problemer som: "4 - (-7)." Denne typen problemer er eksempler på det vi kan kalle doble negativer.
- 2Endre back-to-back "minuser" til en "pluss pluss". I stedet for 4 - (-7), har vi 4 + (7).
- 3Verdier vil hope seg opp. Dumpe alle chips (de bør alle være svart på dette punktet) i en stor haug.
- 4Ditt svar vil være positiv.
- Eksempel: 4 - (-7) blir 4 + (7), eller rettere sagt, 4 + 7, som er lik 11.
- Eksempel: 15 - (-3) blir 15 + (3), eller snarere 15 + 3, som er lik 18.
- 5Se etter feil. Hvis det første tallet er negativt, du enten gjorde et tegn feil eller du har en "trippel negativ", ikke en "double negative" typen problem.
Del fire: beregning av en grave ned problem
- 1Se etter problemer som "-4 -. 7" Dette er ikke en "double negative" fordi minuser er ikke back-to-back.
- Denne typen problemer er noen ganger kalt "grave ned" fordi det er hvordan det kan bli visualisert. Du begynner med jevnt underlag, grave ned fire fot (det er -4), deretter grave ned en annen 7 fot (som er trukket 7). Sluttresultatet: Du er ned 11 ft Derfor -4 til 7 = -11.
- 2Ikke avbryt for å "pluss pluss".
- 3Vil skrive subtraksjon som å legge et negativ. For eksempel, -4 til 7 blir -4 + (-7).
- 4Hoper seg opp verdiene. Dumpe alle chips (de bør være helt rød på dette punktet) i en stor haug.
- 5Endre svaret til negativ.
- Eksempel: -18 til 5 blir -18 + (-5), som tilsvarer -23.
- Eksempel: -4 til 7 blir -4 + (-7), noe som tilsvarer -11.
Del fem: beregning enkle subtraksjon problemer
- 1Se etter problemer som "4-7" eller "7 -. 4"
- 2Endre subtraksjon til å legge en negativ. Derfor, 4 - 4 + 7 blir -7.
- 3Avbryt verdiene. Fjern en rød brikke for hver av svart chip før du går tom for en farge eller den andre.
- 4Avgjøre om svaret er positivt eller negativt. Hvis haug av svarte brikker er større, er svaret positivt, hvis den røde haugen er større, er svaret negativt.
- Eksempel: 6-19 blir 6 + (-19), noe som tilsvarer -13.
- Eksempel: 12 - 30 blir 12 + (-30), noe som tilsvarer -18.
- 5Hvis det første tallet er større enn den andre, som "7-4", så det er bare standard subtraksjon: 7-4 = 3. Du kan skrive det som 7 + (-4), men du trenger ikke å.
- Eksempel: 38-15 kunne bo som er, eller det kan bli 38 + (-15), men uansett får du 23.
Tips
- Tillegg forblir tillegg. Bare subtraksjon er omskrevet som en motsatt.
- Legg merke til at verdien hauger opp. Som refererer til absolutte verdi her. For eksempel sier jeg at -4 + (-7) "hauger opp" til -11. Vi vet alle at -11 er teknisk mindre enn både -4 og -7. Men jeg er interessert i det visuelle referanser - en stor haug av røde chips. Derfor sier jeg at verdien av -4 + (-7) hauger opp.
- Tenk på følgende tabell:
| gir 11 | gir -11 | gir -3 | gir 3 |
|---|---|---|---|
| 4 + 7 | -4 + (-7) | 4 + (-7) | -4 + 7 |
| 4 - (-7) | -4 Til 7 | 4 - 7 | -4 - (-7) |
| 7 - (-4) | -7-4 | -7 - (-4) | 7-4 |
Relaterte wiki hows
- Hvordan legge til
- Hvordan trekke fra
- Hvordan legge til eller trekke fra brøker med vedisk matematikk
- Hvordan legge til et stort antall
- Hvordan trekke fra virkelig fort når omgruppering er nødvendig
