Hvordan finne matematiske sannsynligheter

Sannsynligheten for en uavhengig hendelse

1. 1
   Tell antall alle særegne og like sannsynlig utfall av eksperimentet. La det være n.
   
2. 2
   Tell antall karakteristiske utfall som representerer forekomsten av hendelsen i spørsmålet. La det være n _e.
   
3. 3
   Beregn resultatet av delingen n _e / n. Det er sannsynligheten for hendelsen.
   
4. 4
   Eksempel: "Finn sannsynligheten for å få et partall etter å ha rullet en die"
   
   • Eksperiment: Rolling en rettferdig terning
   • Event: Komme et partall
   • Trinnene ovenfor:
     1. Karakteristiske resultater: 1, 2, 3, 4, 5, 6 ligger alle resultatene, deres telle n = 6
     2. Utfall representerer hendelsen: 2, 4, 6 er alle like tall du kan få, deres teller n _e = 3
     3. Sannsynlighet: P = n _e / n = 3/6 = 0,5 eller 1/2

     Sannsynligheten for uavhengige hendelser forekommer sammen / samtidig

     1. 1
        Finner den enkelte sannsynligheten for at hver hendelse av seg selv.
        
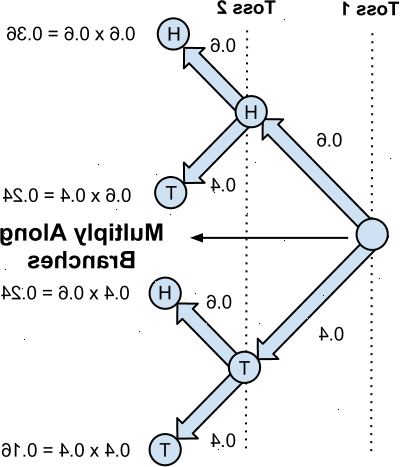
     2. 2
        Multipliser de enkelte sannsynligheter for å finne sannsynligheten for alle av dem skjer sammen.
        
     3. 3
        Eksempel: "En terning kastes, en mynt er kastet, og en spinner med tallene 1 til 5 er spunnet Finn sannsynligheten for å få et tre, et hode og en 4 på terningen, mynt og spinner henholdsvis samtidig.. "
        
        1. Individuelle sannsynligheter:
           1. Får en 3 når rulle en terning: P ₁ = 1/6 (ved hjelp av metoden ovenfor)
           2. Får et hode når kaste en mynt: P ₂ = 1/2
           3. Får en 4 når en spinner er spunnet: P ₃ = 1/5
        2. Sannsynlighet: P = P ₁ * P ₂ * P ₃ = 1/6 * 1/2 * 1/5 = 1/60

        Sannsynligheten for avhengige hendelser

        1. 1
           Beregne sannsynligheten for det første arrangementet. I nesten alle tilfeller, det er en eller flere hendelser som andre hendelser er avhengige av. Dette bør være ditt første til å beregne. Det er uavhengig av seg selv slik at den første delen gjelder.
           
        2. 2
           Identifiser forandring at den første hendelse gjort på miljøet av forsøket. Vanligvis i slike situasjoner, forekomsten av den første hendelsen enten begrenser eller øker antall mulige utfall av eksperimentet.
           
        3. 3
           Beregne sannsynligheten for den andre hendelsen (det tilfelle at an umiddelbart på eller følger umiddelbart etter den første hendelse) ved hjelp av metoden i den første seksjon i lys av de endrede identifisert i to.
           
        4. 4
           Terpe trinn 2 og 3 for påfølgende hendelser, identifisere forandringen gjort av de tidligere hendelsene deretter beregne sannsynligheten for den nye hendelsen i lys av denne forandringen.
           
        5. 5
           Multipliser alle sannsynlighetene du beregnet i foregående trinn, som vil være sannsynligheten for de avhengige hendelser helt.
           
        6. 6
           Eksempel: "Det er en pose med fem grønne kulene, to røde, og 3 blå Hva er sjansen for at to blå kuler og deretter en rød marmor er valgt tilfeldig fra posen.?"
           
           1. Første hendelse: velge en blå marmor (den første i de to blå klinkekuler til å bli valgt først)
              1. Karakteristiske utfall av eksperimentet: 5 grønne + 2 rød + 3 blå = 10 klinkekuler
              2. Utfall representerer event: 3 blå
              3. P ₁ = 3/10
           2. Endre gjort etter hendelse 1: antall utfall endret til fem grønne + 2 røde + 2 blå = 9 klinkekuler.
           3. Andre hendelsen: å velge en blå marmor, med sannsynligheten for to blå kuler / 9 totalt = 2/9
           4. Endring av arrangementet 2: antall utfall endret til 5 grønn + 2 rød + en blå = 8 klinkekuler
           5. Tredje hendelse: velger en rød marmor, med sannsynligheten for to røde kuler / 8 totalt = 1/4
           6. Total sannsynlighet: P _total = P ₁ * P ₂ * P ₃ = 3/10 * 2/9 * 1/4 = 6/360 = 1/60

           Begreper og definisjoner

           • Uavhengige hendelser: er to hendelser som ikke påvirker hverandre. For eksempel ikke kast av en terning ikke påvirke resultatet av rullen av en annen dør eller kaste en mynt.
           • Avhengige hendelser: påvirker hverandre. For eksempel, hvis en marmor er tatt ut av en pose og er ikke skiftes ut, påvirker det sjansene for at en viss marmor ville bli trukket ved.
           • Eksperimentet: er den generelle konteksten som arrangementet er å forekomme. Med andre ord, er det rekken av handlinger som skal utføres på miljøet som fører til forekomsten av hendelser. For eksempel kaster en mynt, rulle en terning, velger en ball fra en sekk eller selv kjører til en viss tilstand. Det hele avhenger av konteksten av problemet.
           • Omgivelsene: er settet av ressurser som blir brukt i eksperimentet. For eksempel, en dør, to mynter, 6 grønne baller, en varebil eller en motorvei gate. Igjen, det kommer an på konteksten av problemet.

           Tips

           • Vær ekstra nøye med å hvert eneste ord i problemstillingen. Se opp for følgende ord og forstå deres eksakte betydning i sammenheng:
             • Og, eller, ikke, men
             • All, for hver, for hver
             • Unntatt
             • "Minst", "på de fleste"
             • "Med", "uten"
             • "Bare hvis", "hvis og bare hvis", "hvis"
           • Beregning avhengige hendelser er lett messed up. Det kan være nyttig hvis du tegner en slags diagram å representere hendelsesforløp og effekten hver enkelt gjør for miljøet av forsøket.