Visualisere to punkter, A og B, forbundet med en rett linje. Nå forestille seg å tegne en ny linje nøyaktig gjennom midten av den første, på nøyaktig 90 grader til den første. Denne andre linjen er en midtnormalen.
Geometrisk sett er en perpendikulær halveringslinje en gruppe punkter (teknisk sett en "locus") som ligger i lik avstand fra både A og B. Formen av gruppen alltid danner en linje. Hvilket som helst punkt på midtnormalen er så langt fra punkt A som fra punkt B. Denne artikkelen beskriver hvordan du finne ligningen midtnormalen, forutsatt at du har koordinatene til punktene A og B.
Trinn
- 1Finn skråningen mellom de to punktene. For informasjon om hvordan du gjør det, kan du se artikkelen Hvordan forstå skråning (i algebra).
- 2Ta at skråningen og finne sin negative gjensidige. Med andre ord, snu brøken igjen, og endre fortegn.
- Eksempel: hvis du starter med 4/9, er den negative gjensidige -9/4.
- Eksempel: hvis du starter med fem, du slår det inn en brøkdel ved å sette en en under det, som dette: 5/1. Deretter er den negative resiproke -1/5.
- Eksempel: hvis du starter med -7/3, er den negative gjensidige 3/7.
- Husk, hvis du starter med en negativ brøkdel, vil den negative gjensidige ender opp positivt!
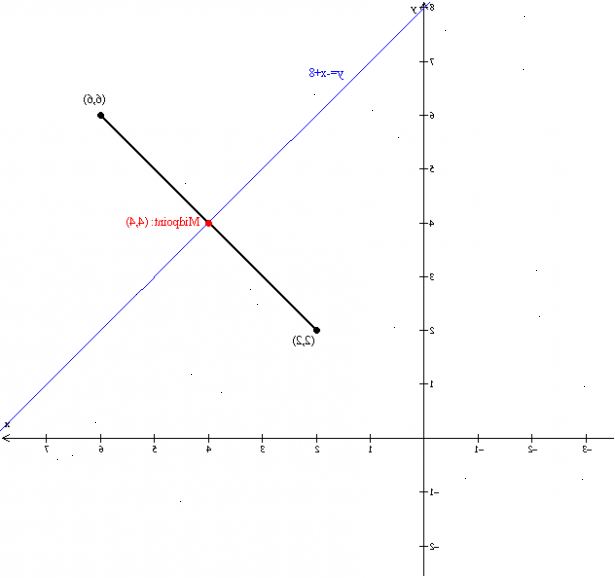
- 3Finn midtpunktet av de to punktene. Midtpunktet ligger på linje fra A til B, halvveis mellom A og B.
- legge til x-koordinaten til A med x-koordinat for B, og deretter dele på to. Dette er den nye x-koordinaten for midtpunktet.
- Legg y-koordinat for A med y-koordinat for B, og deretter dele på to. Dette er y-koordinaten for midtpunktet.
- 4Ved hjelp av dette midtpunkt, og den negative resiproke fra trinn 2, beregne ligningen for linjen. For mer informasjon om hvordan du gjør dette, se artikkelen Hvordan finne ligningen for en linje.
