Rettvinklet trig er nyttig når du arbeider med trekanter og er en fundamental del av trigonometri generelt. Vanligvis er rett trig en student første møte med trig, og det kan være litt forvirrende i starten. Disse trinnene vil avklare trigonometriske forholdstall og hvordan de brukes.
Trinn
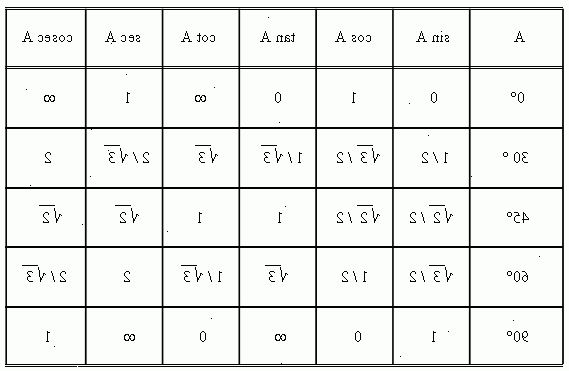
- 1Vet de seks trigonometriske forholdstall. Du må huske på følgende:
- sinus
- forkortet som synd
- motsatt / hypotenusen
- cosinus
- forkortet til cos
- tilstøtende / hypotenusen
- tangent
- forkortet til tan
- motsatt / tilstøtende
- sekans
- forkortet til CSC
- hypotenusen / motsatt
- sekant
- forkortet til sek
- hypotenusen / tilstøtende
- cotangent
- forkortet til barneseng
- tilstøtende / motsatt
- sinus
- 2Oppdage mønstre. Ikke bekymre deg hvis du er forvirret om hva alt betyr akkurat nå og ikke frik ut om memorere alt. Det er ikke så vanskelig hvis du vet mønstrene:
- Forkortelsene er alltid brukes når du skriver ut de trigonometriske funksjoner. Du vil aldri skrive ut cotangent eller sekant. Når du ser forkortelsen, bør du hører navnet. Likeledes når du hører navnet, bør du høre forkortelsen. Legg merke til at i hvert fall unntatt CSC (sekans), er forkortelsen de tre første bokstavene i navnet. CSC er et unntak fordi de tre første bokstavene er "cos" som allerede er brukt. Så i stedet er det de tre første konsonanter.
- Du kan huske de første tre prosenter av følgende: Sohcahtoa. Bare tenk på det som et navn å huske. Gjør ham en Aztec Chieftain hvis det hjelper deg å huske det, bare sørg for at du husker hvordan å stave det. Det er i utgangspunktet den første bokstaven i "s i o synd> pposite h ypotenuse, c hypotenusen,> os en djacent h tilstøtende> ypotenuse, t en o tan> pposite en djacent" Legg merke til at hvis du setter inn ordet løpet mellom to ord som er ikke trigonometriske forhold (dvs. tilstøtende og hypotenusen, ikke cos og tilstøtende), etter navnet på hver trigonometrisk funksjon er dens ratio.
- De tre siste er bare reciprocals av de tre første (ikke invers). Husk at alt uten prefikset "co" har en gjensidig med prefikset, og noe med et prefiks "co" har en gjensidig funksjon uten prefikset. Derfor CSC, sek, og barneseng trigonometriske forholdstall er de resiproke av sin, cos og tan forholdstall henholdsvis. For eksempel er barneseng er forholdet tilstøtende enn motsatt.
- Forkortelsene er alltid brukes når du skriver ut de trigonometriske funksjoner. Du vil aldri skrive ut cotangent eller sekant. Når du ser forkortelsen, bør du hører navnet. Likeledes når du hører navnet, bør du høre forkortelsen. Legg merke til at i hvert fall unntatt CSC (sekans), er forkortelsen de tre første bokstavene i navnet. CSC er et unntak fordi de tre første bokstavene er "cos" som allerede er brukt. Så i stedet er det de tre første konsonanter.
- 3Vet de delene av trekanten. Du vet sikkert hva hypotenusen er på dette punktet, men du kan være litt forvirret om det motsatte og tilstøtende sider. Se på følgende diagram: Disse sidene er korrekt når du bruker vinkel C. Hvis du ønsker å bruke vinkel A, ville ordene motsatte og tilstøtende være snudd i diagrammet.
- 4Forstå hva de trigonometriske forholdstall er og når de brukes. Når rettvinklet trig ble først oppdaget, ble det innsett at når du har to rettvinklede trekanter som ligner (som betyr vinkelen tiltakene er de samme), hvis du deler den ene siden av en annen og gjøre det samme med de tilsvarende sidene av den andre trekanten, vil du få de samme verdiene. De trigonometriske funksjonene ble deretter utviklet slik at du kan finne forholdet for enhver vinkel. Siden navn ble også gitt for å gjøre det lettere å bestemme hvilke vinkler til bruk. Du kan bruke trigonometriske forhold for å fastsette en side tiltaket gitt en av sidene og en vinkel, eller du kan bruke dem til å bestemme en vinkel tiltak gitt to sidelengder.
- 5Finne ut hva du ønsker å løse. Marker ukjent verdi med en "x". Dette vil hjelpe deg å sette opp ligningen senere. Kontroller også at du har nok informasjon til å løse trekanten. Du trenger enten en vinkel og en side eller alle tre sider.
- 6Sett opp forholdet. Etiketten den motsatte side, idet motstøtende side-og hypotenus i forhold til den vinkel markert (det spiller ingen rolle om merket er et tall eller en "x" fra forrige trinn). Deretter skrive ned hvilke sider du enten vet eller ønsker å finne. Uten tanke på CSC, sek, eller barneseng, bestemme hvilken ratio innebærer både av sidene du skrev ned. Du bør ikke bruke den gjensidige forhold fordi det er vanligvis ingen kalkulator knappen for dem. Selv om du kunne, vil det nesten aldri være en situasjon der du må bruke dem til å løse en rettvinklet trekant. Når du vet hvilke forhold du skal bruke, skrive det ned, etterfulgt av verdi eller variabel i trekanten. Deretter skrive et likhetstegn etterfulgt av sidene forholdet omfatter (fremdeles i form av motsatte, tilstøtende, og hypotenusen). Skriv om ligningen, fylle ut side lengder / variabel i forholdet.
- 7Løs ligningen. Hvis variabelen er utenfor trigonometrisk funksjon (det betyr at du var løse for en side), så bare løse for den eksakte verdien av x og koble uttrykket inn i kalkulatoren for en desimal tilnærming til side lengden. Hvis variabelen er inne argumentet i trigonometrisk funksjon (det betyr at du var løse for en vinkel), så bør du forenkle uttrykket på høyre og koble den inverse av at trigonometrisk funksjon fulgt av uttrykket. For eksempel, hvis ligningen var sin (x) = 2/4, så ville forenkle høyre side for å få 1/2, deretter slag i din kalkulator "synd -1" (det er alle én knapp, vanligvis det andre alternativet for den trigonometriske funksjonen du ønsker) etterfulgt av 1/2. Pass på når du gjør beregninger, er du i riktig modus. Hvis du ønsker grader, sette kalkulatoren i grader-modus, hvis du ønsker radianer, sette kalkulatoren i radian-modus, hvis du ikke vet hva grader eller radianer, sette kalkulatoren i grader-modus. Verdien av x er verdien av side-eller vinkel du forsøkte å finne.
Tips
- synd -1 er ikke det samme som CSC, er cos -1 ikke det samme som sek, og tan -1 er ikke det samme som barneseng. Den første er den inverse trigonometriske funksjonen, noe som betyr at hvis du putter i verdien av et forhold, vil det gi deg den tilsvarende vinkelen, det andre er den gjensidige funksjon som betyr at forholdet er snudd.
- Verdiene av sin og cos alltid er mellom -1 og 1, men tangens kan være hvilket som helst tall. Hvis du får en feil på den inverse trigonometriske funksjonen, er verdien trolig for stor eller for liten. Sjekk din ratio og prøv igjen. En vanlig feil er å snu sidene i forholdet, for eksempel ved hjelp hypotenusen / motsatt for synd.
