Wkono

Hvordan beregne lager korrelasjonskoeffisient

Det er ofte nyttig å vite om to aksjer har en tendens til å flytte sammen. For en, vil du ønsker aksjer som ikke er nært beslektet. The Pearson Korrelasjonskoeffisient bidrar til å måle nærhet av avkastningen.

Trinn

Hvordan beregne lager korrelasjonskoeffisient. Beregne gjennomsnittet.
Hvordan beregne lager korrelasjonskoeffisient. Beregne gjennomsnittet.
  1. 1
    Begynn med et sett av n aksjeavkastning, for to bestandene X og Y:
    1 X, X 2,... X er N og Y 1, 2 Y,... Y n
  2. 2
    Beregne gjennomsnittet av hvert sett:
    M x = (X 1 + X 2 +... + X n) / n
    Min = (Y 1 + Y 2 +... + Y n) / n
  3. 3
    Beregn kovariansen:
    KOVARIANS = {(X 1 M-x) (Y-1 M y) + (2-x M x) (Y 2-M y) +... + (n-X M x) (y N-M y )} / n
  4. 4
    Beregn variansen av hvert lager:
    V x = {(X 1-M x) 2 + (X 2-M x) 2 +... + (X n-M x) 2} / n
    V y = {(Y 1-M y) 2 + (Y 2-M y) 2 +... + (Y n-M y) 2} / n
  5. 5
    Standardavviket er kvadratroten av variansen:
    S x = SQRT (V x)
    S y = SQRT (V y)
  6. 6
    Endelig Pearsons korrelasjonskoeffisient:
    Korrelasjon = KOVARIANS / (S x S y)
  7. 7

    Plott parene å få et spredningsdiagram. (En X, Y-1), (2 X, Y 2),... (X n, Y n). Legg merke til noen andre egenskaper av dataene.
    • Den beste tilpasning til data kalles .
    • Korrelasjonen er et mål på hvor tett de to aksjeavkastning er i slekt, lineært. Det er, hvor tett de returnere verdier tilfredsstille en lineær sammenheng som
      Y = βX + α
      for noen konstanter α og β.
    • Kvadratet av korrelasjonen, kalt R-kvadrat, brukes også for å måle hvor tett de returnerer er lineært relatert.
    • Konstantene er forbundet med regresjonslinjen også navn kjent for mange:
      β = beta, α = Alpha.
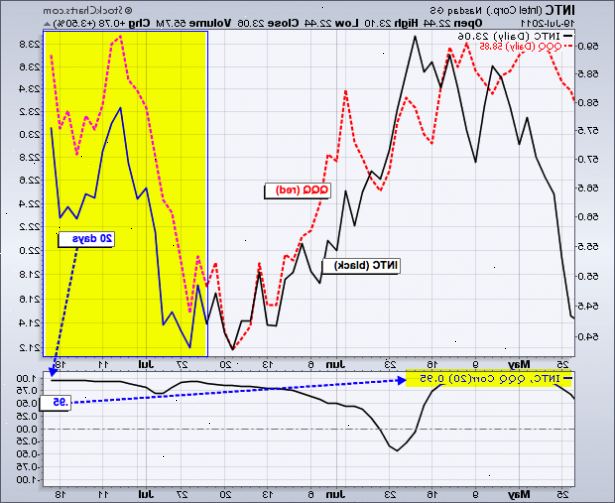
  8. 8
    Her er et eksempel. Den viser hvordan avkastningen av GE lager relateres til avkastningen til S & P 500-indeksen. De blå data er punktplottet og den røde linjen er regresjonslinjen.