Hvordan å faktor annengrads polynom (kvadratiske likninger)

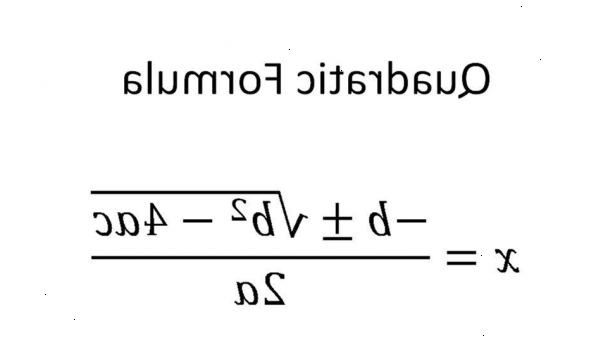
1. 1
   Sett opp uttrykket. Bestill tallene fra høyeste til laveste makt og deretter faktor ut den største felles faktor hvis det finnes.
   6 + 6x ² + 13x
   6x ² + 13x + 6
2. 2
   Finn den priset form ved hjelp av en av metodene nedenfor.
   (2x + 3) (3x +2)
   
3. 3
   Kontrollere arbeidet ved å multiplisere ut hvilke faktorer som bruker folie. Deretter kombinere like vilkår, og du er ferdig!
   (2x + 3) (3x +2)
   6x ² + 4x + 9x + 6
   6x ² + 13x + 6
   

Prøving og feiling metoden

Hvis du har en ganske enkel polynom, vil du være i stand til å finne ut hvilke faktorer selv. MERK: Ved hjelp av denne metoden kan ikke være så enkelt som når factoring mer kompliserte trinomials.

Eksempel: 3x ² + 2x - 8

1. 1
   Liste faktorene til et begrep og c sikt.
   a = 3 faktorer: 1 og 3
   c = -8 faktorer: 2 og 4 eller 1, og 8
   
2. 2
   Skriv ned to sett med parenteser med tomme plasser som dette:
   (X) (x)
   
3. 3
   Fylle mellomrom i fronten av x-ene med et par mulige faktorer av en verdi. Det er bare én mulighet for vårt eksempel:
   ( 3x) ​​( 13x) (x)
   
4. 4
   Fyll ut de to mellomrom etter x-tallet med et par faktorer for den konstant. La oss si vi velger (3x 8) (x 18) (x).
   
5. 5
   Bestem hva skiltene skal være mellom x og tallene. Her er en guide:
   Hvis ax ² + bx + c da (x + h) (x + k)
   Hvis ax ² - bx - c eller ax ² + bx - c da (x - h) (x + k)
   Hvis ^to øks - bx + c da (x - h) (x - k)
   For vårt eksempel 3x ² + 2x - 8 så (x - h) (x + k)
   Vi må gjette så for resten. (3x + 8) (x - 1)
   
6. 6
   Teste et valg ved å multiplisere (bruk folie) de to parentes sammen. Hvis midten sikt er ikke minst riktig verdi (ikke hensyntatt positive eller negative) du har valgt feil c faktorer.
   (3x + 8) (x - 1)
   3x ² - 3x + 8x - 8
   3x ² + 5x - 8 ≠ 3x ² + 2x - 8
   
7. 7
   Bytt ut dine valg hvis det er nødvendig. I vårt eksempel, la oss prøve 2 og 4 i stedet for en og 8: (3x + 2) (x - 4)
   
   • Nå er vår c Begrepet er en -8.
   • Men vår ute / inne combo er-12x og 2x, som ikke vil kombineres for å gjøre det riktige b løpetid på 2 x.
8. 8
   Snu rekkefølgen hvis nødvendig. La oss prøve å flytte to og fire rundt: (3x + 4) (x - 2)
   
   • c Begrepet er fortsatt ok.
   • Ute / inne combo er-6x og 4x. Hvis vi kombinerer dem, får vi ganske nær til 2x vi var ute etter --- rett mengde, feil fortegn.
9. 9
   Dobbeltsjekk at skiltene om nødvendig. Vi kommer til å feste med samme rekkefølge, men swap hvilken som har subtraksjon: (3x - 4) (x + 2)
   
   • c Begrepet er fortsatt ok.
   • Ute / inne combo er nå 6x og-4x. Dette vil kombineres for å skape den positive 2x fra det opprinnelige problem, slik at disse er de riktige forhold.

Nedbryting metoden

Hvis tallene er store, eller er du bare lei av gjetting bruke denne metoden.

Eksempel: 6x ² + 13x + 6

1. 1
   Multipliser en sikt (6 i eksempelet) av den C-sikt (6 også i eksempelet).
   6 • 6 = 36
   
2. 2
   Finn to tall som når multiplisert lik dette tallet (36) og legger opp til å være b sikt (13).
   4 • 9 = 36 4 + 9 = 13
   
3. 3
   Erstatte de to tallene du får inn i denne form som k og h (rekkefølge spiller ingen rolle): ax ² + kx + hx + c
   6x ² + 4x + 9x + 6
   
4. 4
   Faktor polynomet av gruppering. Organiser ligningen slik at du kan ta ut den største felles faktor av de første to begrepene og de siste to vilkår. Begge priset grupper bør være den samme. Legg GCF er sammen og legge dem i parentes ved siden av priset gruppen.
   6x ² + 4x + 9x + 6
   2x (3x + 2) + 3 (3x +2)
   (2x + 3) (3x +2)
   

Triple play metode

Det er svært lik den spaltning metoden, men det er enklere.

Eksempel: 8x ² + 10x + 2

1. 1
   Multipliser et begrep (8 i eksempelet) ved c sikt (2 i dette eksempelet).
   8 • 2 = 16
   
2. 2
   Synes de to nummer som i produktet er dette tall (16) og hvis sum er lik b sikt (10).
   2 • 8 = 16 8 + 2 = 10
   
3. 3
   Ta disse to tall (som vi vil kalle h og k) og erstatte dem inn i dette uttrykket:
   (Ax + H) (ax + K)
   en
   (8x + 8) (8x + 2)
   8
   
4. 4
   Se å se hvilken av de to parentes vilkår i telleren er delelig med en {i dette eksempelet er det (8x + 8)}. Dele dette begrepet av en og la den andre som er.
   (8x + 8) (8x + 2)
   8
   Svar: (x + 1) (8x + 2)
   
5. 5
   Ta GCF (hvis noen) av den ene eller begge parenteser.
   (X + 1) (8x + 2)
   2 (x + 1) (4 x + 1)
   

Forskjell på to firkanter

1. 1
   Faktor ut en GCF hvis du må.
   27x ^2-12
   3 (9x ^2-4)
   
2. 2
   Avgjøre om ligningen er en forskjell på rutene. Det må ha to begrepene og du bør være i stand til å ta kvadratroten av vilkårene jevnt.
   √ (9x ²⁾ = 3x og √ (4) = 2 (legg merke til at vi har utelatt den negative fortegn)
   
3. 3
   Sett a og c verdier fra ligningen din inn i dette uttrykket:
   (√ (a) + √ (c)) (√ (a) - √ (c))
   3 [(√ (9x ²⁾ + √ (4)) (√ (9x ²⁾ - √ (4))]
   3 [(3x + 2) (3x - 2)]
   

Ved hjelp av den kvadratiske formelen

Hvis alt annet mislykkes, og ligningen ikke vil ta hensyn jevnt bruke den kvadratiske formelen.
Eksempel: x ² + 4x + 1

1. 1
   Plugg de tilsvarende verdiene i den kvadratiske formelen:
   x =-b ± √ (b ² - 4ac)
   2a
   x = -4 ± √ ^{(2 til} 4 april • 1 • 1)
   2 • 1
   
2. 2
   Løse for x. Du bør få to x-verdier.
   x = -4 ± √ (16-4)
   2
   x = -4 ± √ (12)
   2
   x = -4 ± √ (4 • 3)
   2
   x = -4 ± 2 √ (3)
   2
   x = -2 ± √ (3)
   x = -2 + √ (3) eller x = -2 - √ (3)
   
3. 3
   Plugg x-verdiene (h og k) i dette uttrykket: (x - h) (x - k)
   (X - (-2 + √ (3)) (x - (-2 - √ (3))
   (X + 2 + √ (3)) (x + 2 - √ (3))
   

Ved hjelp av en kalkulator

Disse retningene er for en TI grafisk kalkulator. Disse er spesielt nyttige i standardiserte tester.

1. 1
   Skriv inn din ligning i [y =]-skjermen.
   y = x ² - x - 2
   
2. 2
   Trykk [grafen]. Du skal se en jevn bue.
   
3. 3
   Lokalisere hvor buen krysser x-aksen. Disse er de x-verdiene.
   (-1, 0), (2, 0)
   x = -1, x = 2
   
   • Hvis du ikke kan identifisere dem ved synet trykk [andre] og deretter [TRACE]. Trykk [2] eller velg "null". Skyv markøren til venstre for en krysser og trykk [ENTER]. Skyv markøren til høyre for en krysser og trykk [ENTER]. Skyv markøren så nært som mulig til den krysser hverandre, og trykk [ENTER]. Kalkulatoren finner den x-verdien. Gjør dette for den andre krysser også.
4. 4
   Plugg x-verdiene (h og k) i dette uttrykket: (x - h) (x - k)
   (X - (-1)) (x - 2)
   (X + 1) (x + (-2)) stort pluss legge det til felles faktor