Velocity er vanligvis funnet ved å dividere forskyvning av tid tatt, men dette resultat representerer den gjennomsnittlige vannhastighet over hele reisen eller tidsperiode. Les denne artikkelen for å finne ut hvordan du kan beregne hastighet over en uendelig liten tidsperiode.
Trinn
- 1Begynn med en vei mindre reiste, fortrengning, til den tiden det tar.
- 2Vi vil kalle forskyvning = s
- 3Tid = t
- 4Velocity = v
- 5Gradient = m
- 6^ Skiltet er "til makt '
- 7(For eksempel) Vekt (s) = 2t ^ 2-4t 7.
- 8Hastighet (v) ved tiden (t) er lik stigningen (endringshastigheten) av den funksjon som relaterer forskyvning (e) til tid (t).
- 9Den deriverte av en funksjon er lik stigningen til funksjonen på noe punkt. For å finne den deriverte du differensiere funksjon som dette:
- 10Hovedregel for å finne deriverte: Hvis y = a * x ^ n
- 11Derivat = a * n * x ^ n-1
- 12Denne regelen brukes på hvert semester av polynomet, vil konstantleddet (begrepet som ikke multipliserer med x variabel) forsvinner fordi det vil bli multiplisert med 0.
- 13Arbeidet eksempel: y = 3x ^ 2 + 4x + 7
- 14Derivat = (3 * 2) * x ^ (2-1) + (4 * 1) * x ^ (1-1) + (7 * 0) * x ^ (0-1)
- 15= 6x ^ 1 + 4x ^ 0 + 0x ^ -1
- 16= 6x + 4
- 17Derfor gradienten i funksjon vil alltid være lik 6x + 4.
- 18For å finne momentan hastighet du vil bruke metoden ovenfor til å skille ligningen om (s) til (t), vil dette gi deg formelen som gjelder hastighet til annen.
- 19For å finne akselerasjonen du ville bruke metoden vist seg å skille ligningen knyttet hastighet til annen, derfor å finne ligningen for akselerasjon må du først finne ligningen for hastighet.
- 20Det følgende er en forklaring på hvor prosessen med differensiering kom fra.
- 21Tenk deg at y-aksen av grafen din er forskyvning skala og x-aksen er tid skala, slik at grafen kan gå under x-aksen, men det vil aldri gå bak y-aksen, ville dette bety å gå tilbake i tid.
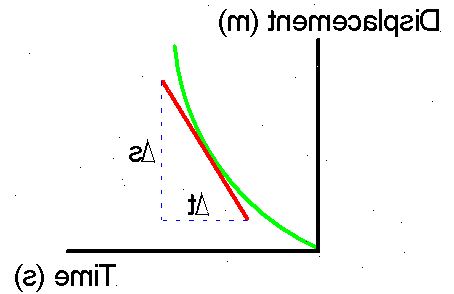
- 22Nå i tankene dine har du en graf. Stigningen av en graf er frekvensen av endring av y dividert med frekvensen av endring av x. Så hvis Y er fortrengning og X er tid, er det gradient endringshastigheten av forskyvning dividert med endringshastigheten av tid, er dette åpenbart hastighet!
- 23Så nå hva vi trenger er å finne gradient av grafen på noe punkt. Jeg kommer til å forklare prosessen fra første prinsipper, kan du hoppe til trinn () hvis du ønsker det.
- 24For å gjøre dette bruker vi et triks som kalles å ta en grense, tar en grense innebærer å ta to punkter P og Q på den buede grafen og finne gradient av linjen knytte dem som avstanden mellom dem blir mindre.
- 25Ta P å være det punktet på grafen hvor X (eller eiendommen på X-aksen) er lik 1, er verdien ikke av betydning, slik at du kan velge et praktisk verdi.
- 26Ta Q for å være det punkt hvor X er lik, for eksempel 3.
- 27Nå arbeider dere ut gradienten mellom P og Q, og forskjellen mellom X-verdi av P og X-verdien av Q heter, for eksempel, H.
- 28Nå kan du redusere H etter litt, IE: bringe Q nærmere p på X-aksen og beregne gradient mellom P og Q. Du vil begynne å se etter noen omregninger at gradient er tending mot en grense, er det sakte komme nærmere en verdi, men vil ikke helt får til det så lenge H> 0. Verdien som gradient er tending mot H som tenderer mot 0 er grensen, blir dette tatt som er lik stigningen av tangenten til den kurve som er kjent for å være parallell med kurven for en uendelig liten tidsperiode. Gradienten til tangenten er derfor gradienten av kurven ved punktet P.
- 29Ligningen for graderingen av tangent kalles avledet ligningen, er dette hvor du finner det algebraisk.
- 30Den deriverte eller deriverte er skrevet som dy løpet dx.
- 31Hvis kraften i X i første begrepet er N, så den deriverte av begrepet er N multiplisert med X til kraften i n-1 er dette gjentas for de øvrige vilkårene i ligningen og konstant sikt, er den uten en X utelatt.
- 32Nå har du en funksjon som gir deg gradient av en funksjon på et bestemt punkt.
- 33Gradienten, i tilfelle av en forskyvning tid-diagram som vi snakker om, er lik hastigheten i enheter på avstand per tidsenhet. Hva gjør denne måte å beregne hastighet spesielle er at det tillater oss å beregne hastighet over en uendelig liten tidsperiode.
Tips
- Forskyvning er som avstand, men det har et sett retning, gjør denne forskyvningen en vektor og hastighet en skalar. Fortrengning kan være negativ, mens avstanden vil bare være positivt.
- Dette Google vil bli bedre når jeg redigerer det.
- Den ligning som relaterer Y (forskyvning) til x (tid) kan være veldig enkelt som for eksempel [Y = 6x + 3], i dette tilfellet den gradienten er konstant, og det er egentlig ikke neccesary å differensiere for å finne gradienten som er selvfølgelig 6.
- Med denne typen arbeid hjelper det egentlig å prøve og visualisere problemet og bruke matematikken når du har bestemt hva eiendommen du trenger å finne.
