Hvordan å faktor trinomials

1. 1
   Faktor ut noen faktorer som er felles for alle tre semestre. Hvis trinomial er konstanter er alle multipler av samme nummer, kan dette tallet være priset ut, eller hvis hver komponent av trinomial viser en vanlig variabel, kan den variabelen bli priset ut.
   

Kvadratiske trinomials

1. 1
   Bestill trinomial med sine argumenter fra størst til minst. Argumentet er variabel i polynomet, den normale orden for notering vilkårene er fra den høyeste makt til det laveste. Dermed 5 + x2 + 6x bør omorganiseres som x ^ 2 + 6x + 5.
   
   • Derfor, i den trinomial 3x2 + 18x + 15, er hver et konstant multiplum av tre, slik at den 3 kan være tatt ut for å gjøre 3 (x2 + 6x + 5).
   • I trinomial - x2 - 2x - 1, hver komponent har blitt multiplisert med -1, som kan være tatt ut og skrives (-1) (x ^ 2 + 2x + 1), eller mer vanlig - (x2 + 2x + 1).
   • I trinomial 3x ^ 2 y + 3xy - 60Y, hver komponent har blitt multiplisert med 3Y, som kan være tatt ut for å gjøre 3y (x ^ 2 + x - 20).
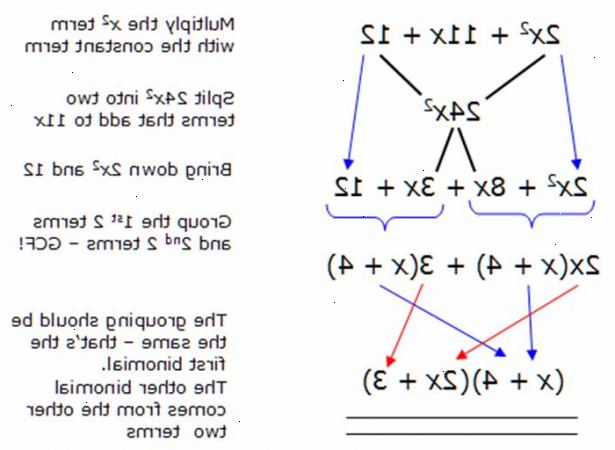
2. 2
   Bryt ned trinomial inn to binomiske faktorer. En binomial er et polynom med to komponenter i form mx + n, der m og n representerer numeriske konstanter. Det første leddet i hver av de to binomiske faktorer vil være en av faktorene til det første leddet i trinomial (ax ^ 2) og det andre leddet av hver av de to binomiske faktorer vil være en av faktorene i tredje periode ( c). Multiplisere det første leddet i den første binomiale ved det andre leddet i den andre binomiale og legge den til produktet av første periode i andre binomiale multiplisert med det andre leddet i den første binomiale skal produsere det andre leddet av trinomial (bx).
   
   • Dermed, for trinomial x ^ 2 + 6x + 5, vil det første leddet i hver binomial faktor være x, fordi x ganger x produserer x ^ 2. De siste vilkårene for hvert binomial faktor er fem og en, fordi fem ganger en lik fem. Den binomiske faktorene er (x + 5) (x + 1), som kan kontrolleres ved å multiplisere det første leddet i den første binomiale ved det andre leddet i den andre binomial, produsere x, og legge det til det andre leddet i den første binomiske ganger det første leddet i den andre binomial, eller 5x, noe som gjør en sum på 6x, det andre leddet i trinomial.
   • Når det er flere mulige faktorer for ett av tallene, har den riktige verdien for hver binomial å være begrunnet ut. For de trinomial x ^ 2 + X - 20, mens det første leddet i hver binomial faktor vil være x, fordi verdien av a i trinomial forstås som en, kan den absolutte verdien av c, 20, være tatt til 20 ganger 1, 10 ganger 2 eller 5 ganger 4. Ser vi på verdien av b, som er en må faktorene i andre periode av hver binomial legge til en. Fordi den virkelige verdi av c er et negativt tall, - 20, er en av faktorene må være negativ, fordi et positivt tall ganger et negativt tall er et negativt tall. Som 5 - 4 (eller 5 pluss - 4) er lik 1, er den riktige par av binomial faktorer (x + 5) (x - 4).

Bestemme riktig binomiske faktorer i spesielle tilfeller

1. 1
   Sjekk om konstant i enten første eller tredje periode av trinomial er et primtall. En primtall kan deles jevnt bare av seg selv og en. Dette reduserer antallet av mulige binomial faktorer. I eksemplet gitt tidligere til x ^ 2 + 6x + 5, fordi 5 er et primtall, er det bare en mulig sett av binomial faktorer, (x + 5) (x + 1).
   
2. 2
   Sjekk for å se om trinomial er en perfekt kvadrat. Perfekte kvadrater er et resultat av tall blir multiplisert med seg selv: 1 * 1 = 1, 2 * 2 = 4, 3 * 3 = 9, og så videre. For trinomial ax ^ 2 + bx + c for å være et perfekt kvadrat, må verdiene for a og c være perfekte firkanter, og verdien av b må være doble verdien av produktet av kvadratroten av a og c.
   
   • Den trinomial x ^ 2 + 6x + 9 er en perfekt kvadrat og kan være priset som (x + 3) (x + 3). Verdien av a er 1, som er en kvadratisk, og verdien av C-er 9, som er 3 i andre, og verdien av b er 6, som er det dobbelte av produktet av kvadratroten av a og c, eller 2 (1 * 3).
   • Den trinomial 4x ^ 2 + 12x + 9 er også et perfekt kvadrat og kan være priset som (2x + 3) (2x + 3). Verdien av a er 4, som er 2 kvadrat, og verdien av c er igjen 9, eller 3 i andre, og verdien av b er 12, det dobbelte av produktet av kvadratroten av a og c, eller 2 (2 * 3 ).
   • Legg merke til at for et trinomial å være en perfekt kvadratisk, må verdiene av a og c alltid være positive tall. Hvis begge er negative, første faktoren ut -1 fra hver term i trinomial å gjøre disse verdiene positiv, som også vil reversere tegn på b fra positiv til negativ, eller negativ til positiv.
3. 3
   Se om "trinomial" er faktisk en factorable binomial. Noen binomials kan være priset inn komponent binomials like trinomials kan. Disse er skrevet i formen ax ^ 2 - c, der a og c er hver perfekte firkanter. (De kan forstås som trinomials hvor verdien av b er null.) Disse binomials faktor inn i binomial par der de første og andre av betingelsene i hver binomial er identiske, med unntak av den første har et tillegg skilt mellom vilkårene og den andre har en subtraksjon signere.
   
   • For eksempel binomisk 4 x ^ 2-9 faktorer i (2x + 3) (2x - 3), fordi to er kvadratroten av 4 og 3 er kvadratroten av ni. Fordi multiplisere en positiv med et negativt tall gir et negativt tall, har en binomial av paret et tillegg tegn i forkant av tre og den andre har en subtraksjon tegn. Multiplisere parene ut produserer 4x ^ 2 + 6x - 6x - 9, eller rett og slett 4x ^ 2 - 9.

Quadratics i en skjult variabel

Noen trinomials kan nominelt ser ut til å være av høy grad, men er egentlig bare kvadratisk. Når de er identifisert, kan de være behandlet slik.

1. 1
   Se på variablene i hvert semester. For eksempel x ^ 6 - 7x ^ 3 + 12 ser ut til å ha grad 6, men etter at substitusjon, u = x ^ 3, blir det u ^ 2 - 7u + 12. Dette gjelder multivariable polynomer også. For eksempel x ^ 5y - forenkler 7x ^ 3y ^ 2 + 12Y ^ 3 til xy ^ 3 (u ^ 2 - 7u + 12) etter substitusjon u = x ^ 2 / y. En slik substitusjon vil være mulig når summen av de grader av to betingelser er to ganger graden av gjenværende sikt.
   
2. 2
   Ved en slik substitusjon kan gjøres, faktor den enklere polynom, i dette tilfellet, u ^ 2 - 7u + 12 = (U-3) (U-4)
   
3. 3
   Angre substitusjonen presentere løsningen i den opprinnelige variabel, x. Det vil si, x ^ 6 - 7x ^ 3 + 12 = (x ^ 3-3) (x ^ 3 - 4). Hvis det er mulig eller ønskelig, ytterligere redusere hver faktor.
   

Eisenstein kriterier

Dette teoremet gjelder for polynomer med en rekke vilkår, men gjelder spesielt lett å trinomials siden de fleste koeffisientene er null. Det er ikke en factoring teknikk, men kan identifisere når et polynom er irreducible.

1. 1
   Finn alle primtall, p, som deler både konstant sikt og mellomlang sikt.
   
2. 2
   For hvert, sjekk følgende to forhold.
   
   • Den konstante term må være et multiplum av p, men ikke et multiplum av p ^ 2.
   • Den ledende sikt må ikke være et multiplum av p.
3. 3
   Hvis det er et primtall som skiller alle koeffisienter bortsett fra den koeffisient ledende, men bare skiller den konstante term en gang, så polynomet er ureduserbart. Eisenstein gjør det mulig å raskt finne ut at 14x ^ 9 + 45x ^ 4 + 51 er irreducible fordi prime 3 deler 45 og 51, men ikke 14 og 9 ikke deler 51.
   

Quadratics i en variabel

Trinomials av høyere grad i flere variabler kan vise seg å være kvadratisk eller lineær i en av variablene.

1. 1
   Vurdere en trinomial som 4x ^ 3y ^ 2 - 5x ^ 4 + 15y. Det er graden 5 i x og y, men bare grad 2 i y.
   
2. 2
   Omskrive som et polynom i den variabelen, behandle alle andre variabler, som koeffisienter. Det vil si, skrive så (4x ^ 3) y ^ 2 + (15) y - (5x ^ 4).
   
3. 3
   Løse for y i form av x ved hjelp av kvadratiske formelen.